Задача 23869 Задание 2. Найти производные функций. В...
Условие
Найти производные функций.
В пункте в) найти вторую производную:
Вариант 9:
а) [m] y = - \sqrt{x} - \operatorname{arctg} \sqrt{x} [/m]
б) [m] y = \cos^3{3x} - \sin^3{3x} [/m]
в) [m] y = x \cdot e^{x^2} [/m]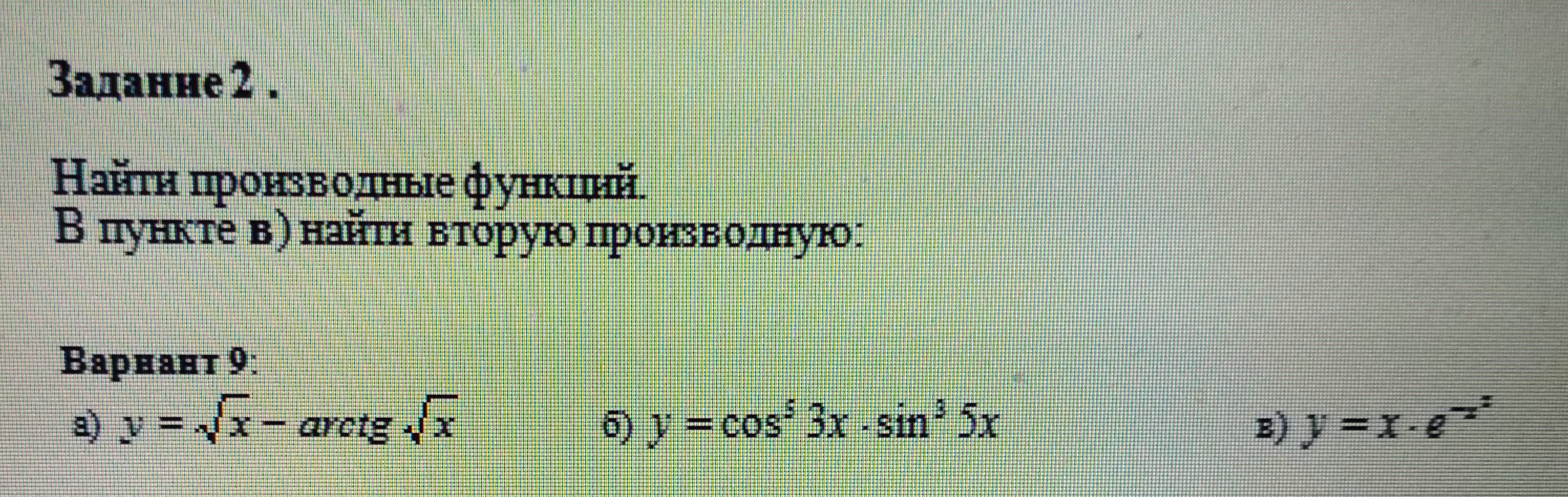
Все решения
=1/(2sqrt(x)) * (1 - (1/(1+х))=х/(2*(1+х)*sqrt(x))
y`=(cos^5(3x))`*sin^3(5x)+cos^5(3x) * (sin^3(5x))`= 5*(cos^43x)*(-sin3x)*3*(sin^35x) + (cos^53x)*(3sin^25x)*(cos5x)*5=
=-15(cos^43x)*(sin3x)(sin^35x)+15(cos^53x)*(sin^25x)*(cos5x)=
=15(cos^43x)*(sin^25x)*(cos3x*cos5x-sin5x*sin3x)=
=15(cos^43x)*(sin^25x)*(cos(5x-3x)=
=15(cos^43x)*(sin^25x)*(cos2x)
y`=(x)`*e^(-x^2)+(x)*(e^(-x^2)`=
=e^(-x^2)+x*(e^(-x^2)*(-x^2)`=
=e^(-x^2)+x*(e^(-x^2)*(-2x)=
=e^(-x^2)*(1-2x^2)
y``=(e^(-x^2))`*(1-2x^2) + (e^(-x^2))*(1-2x^2)`=
=(e^(-x^2))*(-x^2)`*(1-2x^2) + (e^(-x^2))*(-4x)=
=e^(-x^2)*(4x^2-6x)