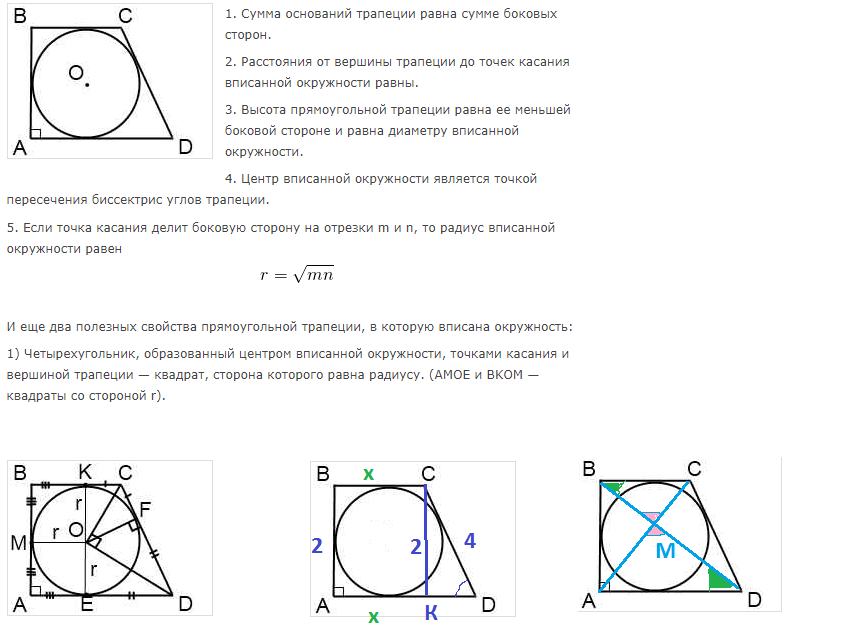
Задача 23867 В прямоугольную трапецию ABCD с большим...

u93157236151

17.02.2018

В прямоугольную трапецию ABCD с большим основанием AD и прямыми углами A и B вписана окружность с центром в точке O.
a) Докажите, что CO^2 +OD^2 = (BC+AD-AB)^2
б) Найдите расстояние от точки пересечения диагоналей трапеции до точки касания вписанной окружности и меньшего основания, если высота трапеции равна 2 и угол ADC равен 30 градусов.

SOVA

17.02.2018

★

1) О - точка пересечения биссектрис.
Сумма углов, прилежащих к боковой стороне CD
равна 180 градусов.
Значит
∠ OCD + ∠ ODC=90 градусов
и ∠ СOD = 90 градусов, треугольник СOD - прямоугольный
По теореме Пифагора
CO^2+OD^2=CD^2
Cм. приложение
По свойству 1^(o)
BC+AD=AB+CD

CD=BC+AD-AB

CO^2 +OD^2 = (BC+AD–AB)^2

2)
Проводим CК ⊥ AD
В прямоугольном треугольнике КCD
катет СК против угла в 30 градусов равен половине гипотенузы CD.
Значит СD=2*CK=4

KD=4*cos30^(o)=4sqrt(3)/2=2sqrt(3)



Пусть ВС=х, AK=x
AB+CD=BC+AD
2+4=x+(x+2sqrt(3))
x=3-sqrt(3)
BC=3-sqrt(3)
AD=3-sqrt(3)+2sqrt(3)=3+sqrt(3)

Из подобия Δ ВСМ и Δ ADM
d/(h-d)=BC/AD

d/(2-d)=(3-sqrt(3))/(3+sqrt(3))

d=(3-sqrt(3))/3