Задача 23755 Решите неравенство...
Условие
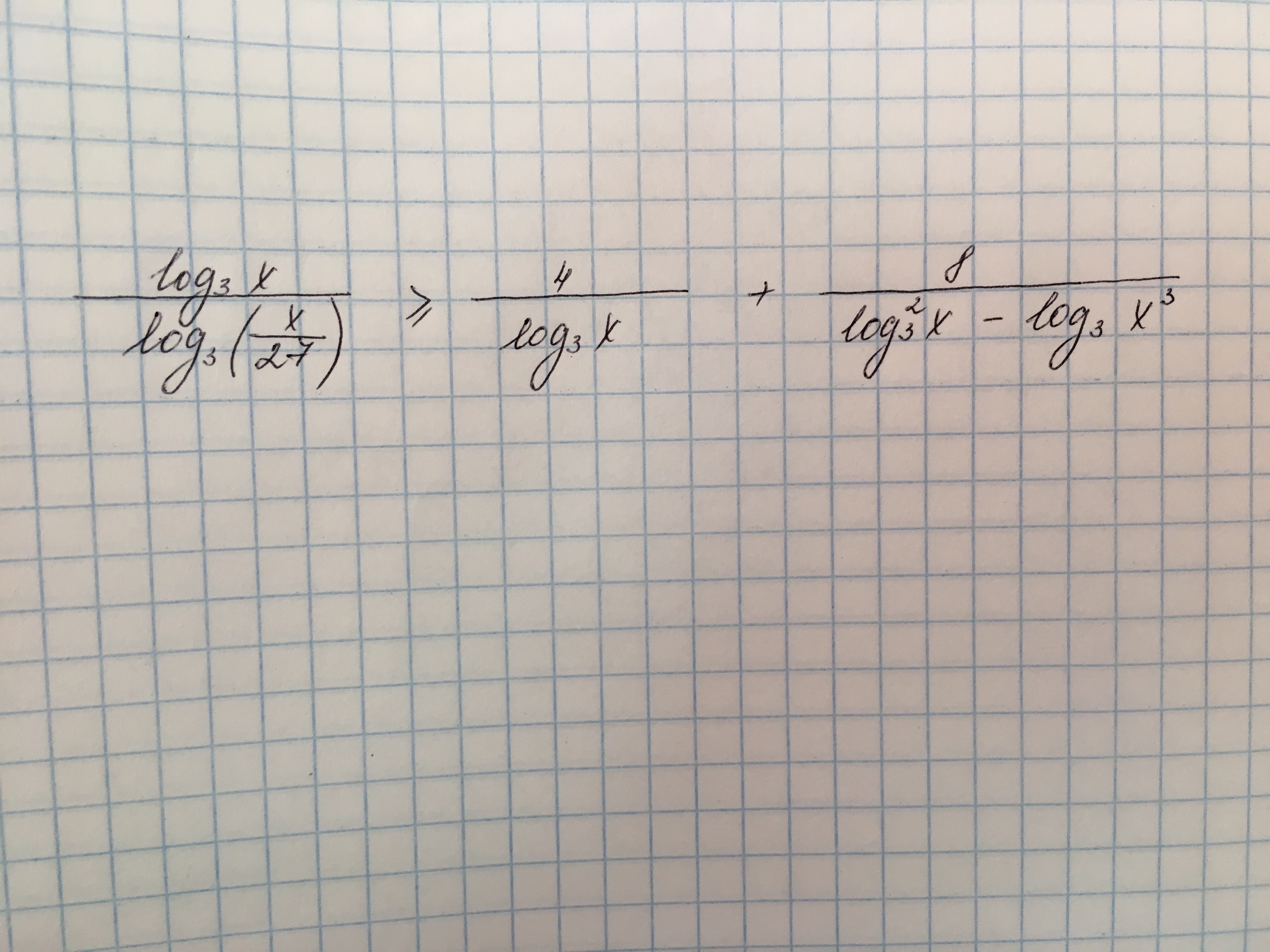
предмет не задан
367
Решение
★
x > 0
Замена переменной
log_(3)x=t
log_(3)(x/27)=t-3
log_(3)x^3=3log_(3)x=3t
t/(t-3) больше или равно (4/t)-(8/(t^2-3t))
(t-2)^2/(t*(t-3)) больше или равно 0
_+__ (0) __-__ [2] _-_ (3) __+__
t < 0 ИЛИ t=2 ИЛИ t > 3
log_(3) x < 0 ИЛИ log_(3) x= 2 ИЛИ log_(3) x > 3
x < 1 ИЛИ х=9 ИЛИ x > 27
С учетом ОДЗ получаем
О т в е т. (0;1) U{9} U(27;+ бесконечность )