Задача 23751 Все на картинке...
Условие
Решение
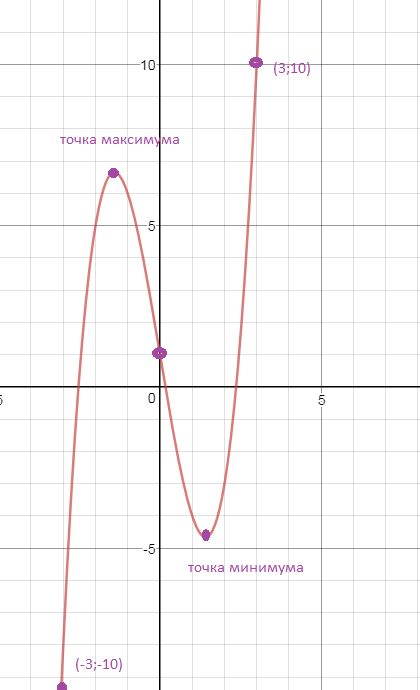
D(y)=(- бесконечность ;+ бесконечность )
Функция не является ни четной, ни нечетной
f(-x)=-x^3+6x+1
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
y`=3x^2-6
y`=0
3x^2-6=0
3(x^2-2)=0
x^2-2=0
x=-sqrt(2) или х=sqrt(2)
_+__ (-sqrt(2)) __-__ (sqrt(2)) ____+__
На (- бесконечность;- sqrt(2)) и на (sqrt(2); + бесконечность)
производная положительна, функция возрастает.
На (-sqrt(2);sqrt(2)) производная отрицательна, функция убывает.
x=-sqrt(2) - точка максимума, производная меняет знак с + на -
y(-sqrt(2))=4sqrt(2)+1
х=sqrt(2) - точка минимума, производная меняет знак с - на +
y(sqrt(2))=-4sqrt(2)+1
y``=6x
При x < 0 вторая производная отрицательна, функция выпукла вверх, при х > 0 вторая производная положительна, функция выпукла вниз
Асимптот нет.
lim_(x бесконечность )= бесконечность
Cм. график и на нем дополнительные точки
2)
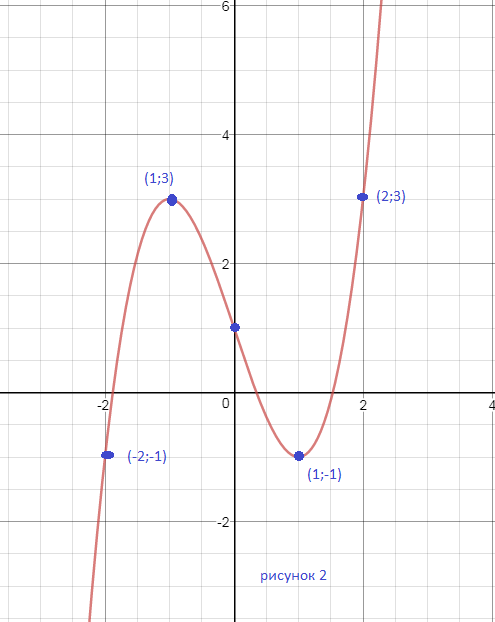
D(y)=(- бесконечность ;+ бесконечность )
Функция не является ни четной, ни нечетной
f(-x)=-x^3+3x+1
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
y`=3x^2-3
y`=0
3x^2-3=0
3(x^2-1)=0
x^2-1=0
x=-1 или х=1
_+__ (-1) __-__ (1) ____+__
На (- бесконечность;- 1) и на (1; + бесконечность)
производная положительна, функция возрастает.
На (-1;1) производная отрицательна, функция убывает.
x=-1 - точка максимума, производная меняет знак с + на -y(-1)=3
х=1 - точка минимума, производная меняет знак с - на +
y(1)=-1
y``=6x
При x < 0 вторая производная отрицательна, функция выпукла вверх, при х > 0 вторая производная положительна, функция выпукла вниз
Асимптот нет.
lim_(x бесконечность )= бесконечность
Cм. график и на нем дополнительные точки
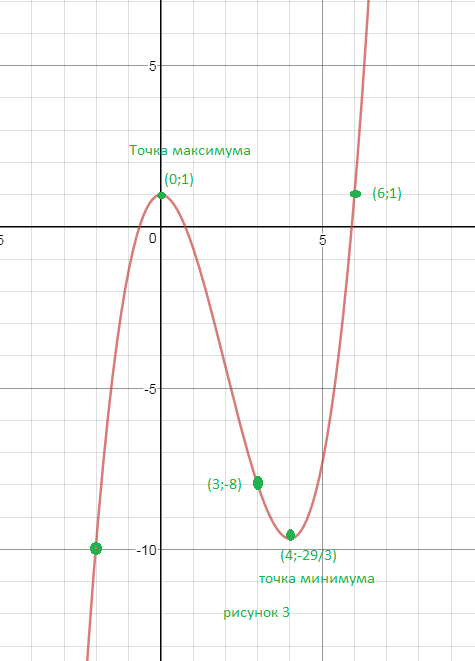
3)D(y)=(- бесконечность ;+ бесконечность )
Функция не является ни четной, ни нечетной
f(-x)=-(1/3)*x^3-2x^2+1
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
y`=x^2-4x
y`=0
x^2-4x=0
x(x-4)=0
x=0 или х=4
_+__ (0) __-__ (4) ____+__
На (- бесконечность;0) и на (0; + бесконечность)
производная положительна, функция возрастает.
На (-0;4) производная отрицательна, функция убывает.
x=0 - точка максимума, производная меняет знак с + на -
y(0)=0
х=4 - точка минимума, производная меняет знак с - на +
y(4)=-29/3
y``=2x
При x < 0 вторая производная отрицательна, функция выпукла вверх, при х > 0 вторая производная положительна, функция выпукла вниз
Асимптот нет.
lim_(x бесконечность )= бесконечность
Cм. график и на нем дополнительные точки
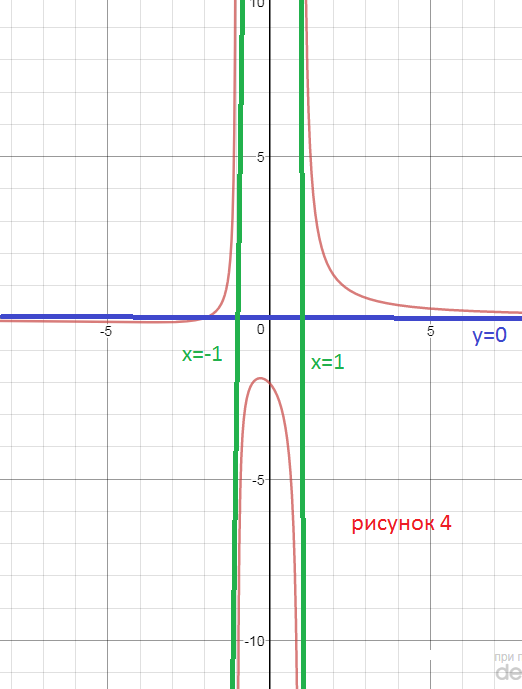
4)
D(y)=(- бесконечность;-1)U(-1;1)U(1:+ бесконечность )
x=-1 и х=1 - вертикальные асимптоты,
lim_(x ± 1)=∞
Функция не является ни четной, ни нечетной
f(-x)=(-x+2)/(x^2-1)
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
y`=((x+2)`*(x^2-1)-(x^2-1)`*(x+1))/((x^2-1))^2
y`=(-x^2-2x-1)/(x^2-1)^2
y`=-(x+1)^2/(x^2-1)^2
y`=0
x=-1
Производная отрицательна, функция убывает.
При x < 0 вторая производная отрицательна, функция выпукла вверх, при х > 0 вторая производная положительна, функция выпукла вниз
Горизонтальная асимптота y=0
lim_(x бесконечность )=0
Cм. график и на нем дополнительные точки
