Задача 23599 ...
Условие
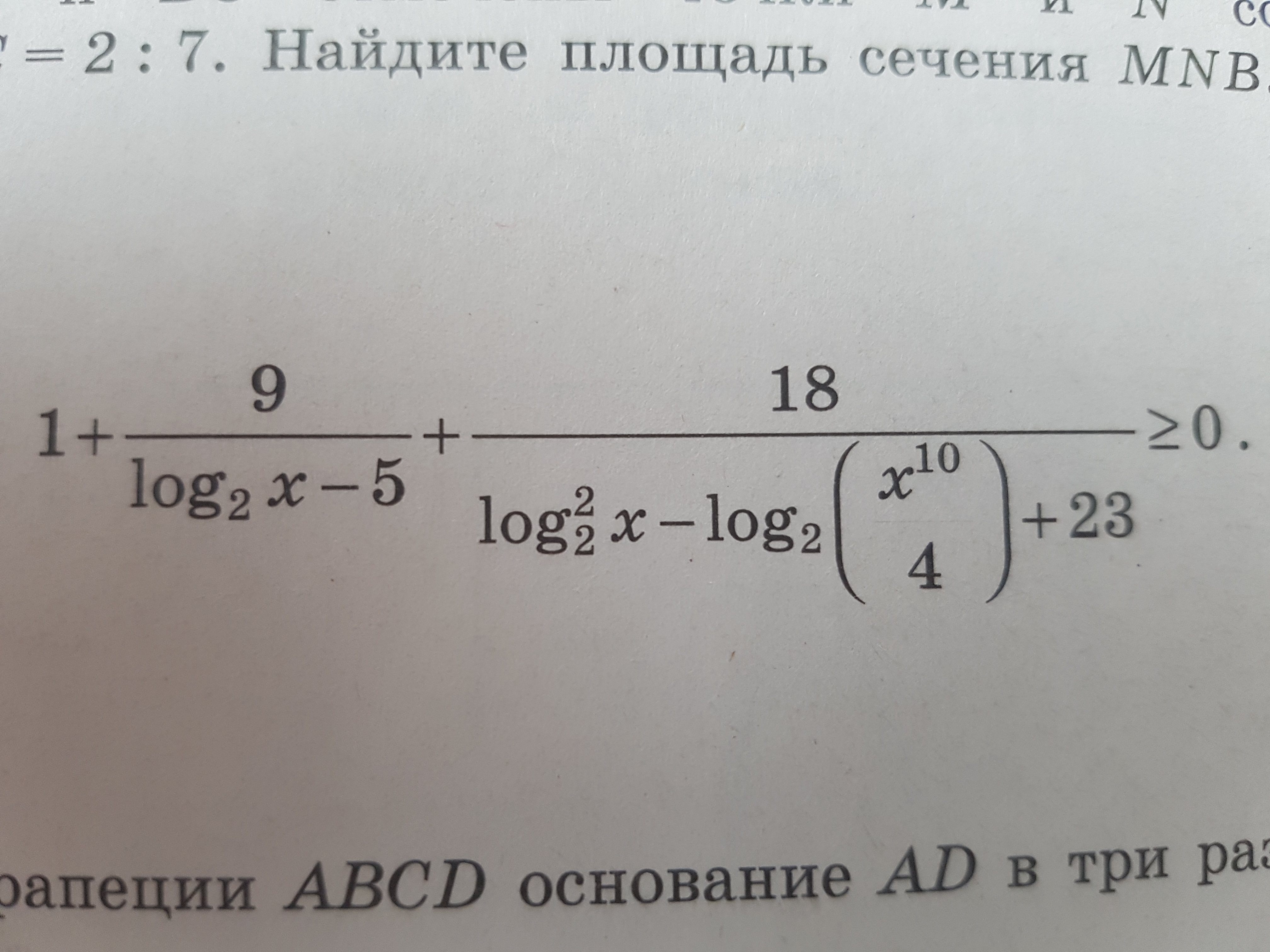
Решение
(условия неравенства знаменателей дробей нулю будут рассмотрены в ходе решения )
Замена переменной
log_(2)x=t
log_(2)(x^(10)/4)=log_(2)x^(10)-log_(2)4=10log_(2)|x| -2
В условиях ОДЗ: x > 0
|x|=x
получим
10 log_(2)x-2=10t-2
Неравенство принимает вид:
1 + (9/(t-5))+(18/(t^2-10t+25)) больше или равно 0
(t^2-t-2)/(t-5)^2 больше или равно 0
нули числителя
t^2-t-2=0
D=1+8=9
t1=-1 или t2=2
Нули знаменателя
t=5
__+__ [-1] ___-__ [2] __+___ (5) __+__
t меньше или равно -1 или 2 меньше или равно t < 5 или t > 5
Обратная замена
log_(2) x меньше или равно -1 ⇒ х меньше или равно 1/2
или
2 меньше или равно log_(2)x < 5 4 меньше или равно х < 32
или
log_(2)x > 5 ⇒ log_(2)x > log_(2) 2^5 ⇒ x > 32
C учетом ОДЗ: х > 0
О т в е т. (0;1/2] U [4;32) U (32; + бесконечность )