Задача 23559 Все на картинке...
Условие
Решение
{x > 0, x ≠ 1 ⇒ (0;1) U (1;+ бесконечность)
{(8-12x)/(x-6) > 0 ⇒ (12х-8)/(x-6) < 0 ⇒ ((2/3);6)
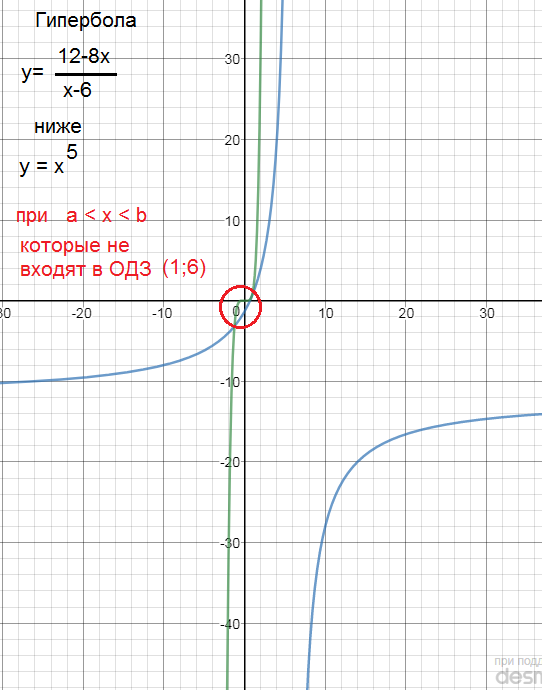
ОДЗ: (1;6)
log_(x)(8-12x)/(x-6) больше или равно 5
log_(x) (8-12x)/(x-6) больше или равно log_(x) x^5
При х > 1 логарифмическая функция возрастает, большему значению функции соответствует большее значение аргумента.
(x-1)*((8-12x)/(x-6) больше или равно x^5
⇒ (x-1)*(x^6-6x^5+12x-8)/(x-6) меньше или равно 0
Если 1 < x < 6
x^6-6x^5+12x-8 < 0
(исследовать функцию
у=x^6-6x^5+12x-8 с помощью производной и построить график)
(x-1)*(x^6-6x^5+12x-8)/(x-6) > 0 при х < 1 или х > 6
Или графическое решение неравенства
(8х-12)/(x-6) больше или равно x^5
О т в е т . Нет решений.
