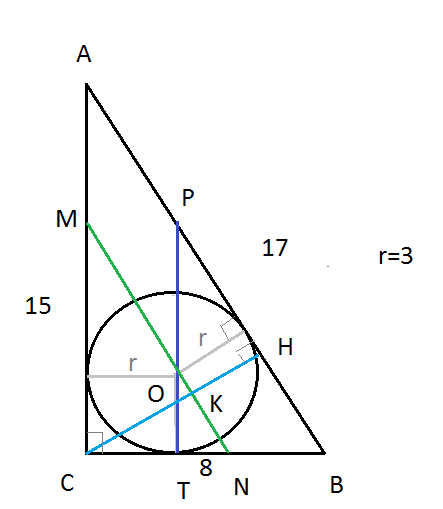
Задача 23203 8. В прямоугольном треугольнике [m] ABC...

u2133192174

01.02.2018

8. В прямоугольном треугольнике [m] ABC [/m] с прямым углом [m] C [/m] гипотенуза равна 17, а катет [m] BC [/m] равен 8. Через точку [m] O [/m] пересечения биссектрис треугольника проведены прямые [m] MN \parallel AB [/m] и [m] PT \parallel AC [m]M \in AC, N \in BC, P \in AB, \ T \in BC [/m]. Найдите длину отрезка [m] MN [/m].

SOVA

02.02.2018

★

По теореме Пифагора
АС^2=AB^2-BC^2=17^2-8^2=289-64=225
AC=15

OT=r(вписанной окр.)=S/p
S=(1/2)AC*BC=(1/2)*15*8=60
p=(15+17+8)/2=20
r=60/20=3

CН=h=2S/AB=120/17
CК=р=h-r=(120/17)-3=69/17

Из подобия треугольников СMN и CAB ( MN|| AB)
MN:AB=CK:CH

MN=AB*CK/CH=69*17/120=1173/120=9 целых 93/120=9 целых 31/40=9,775