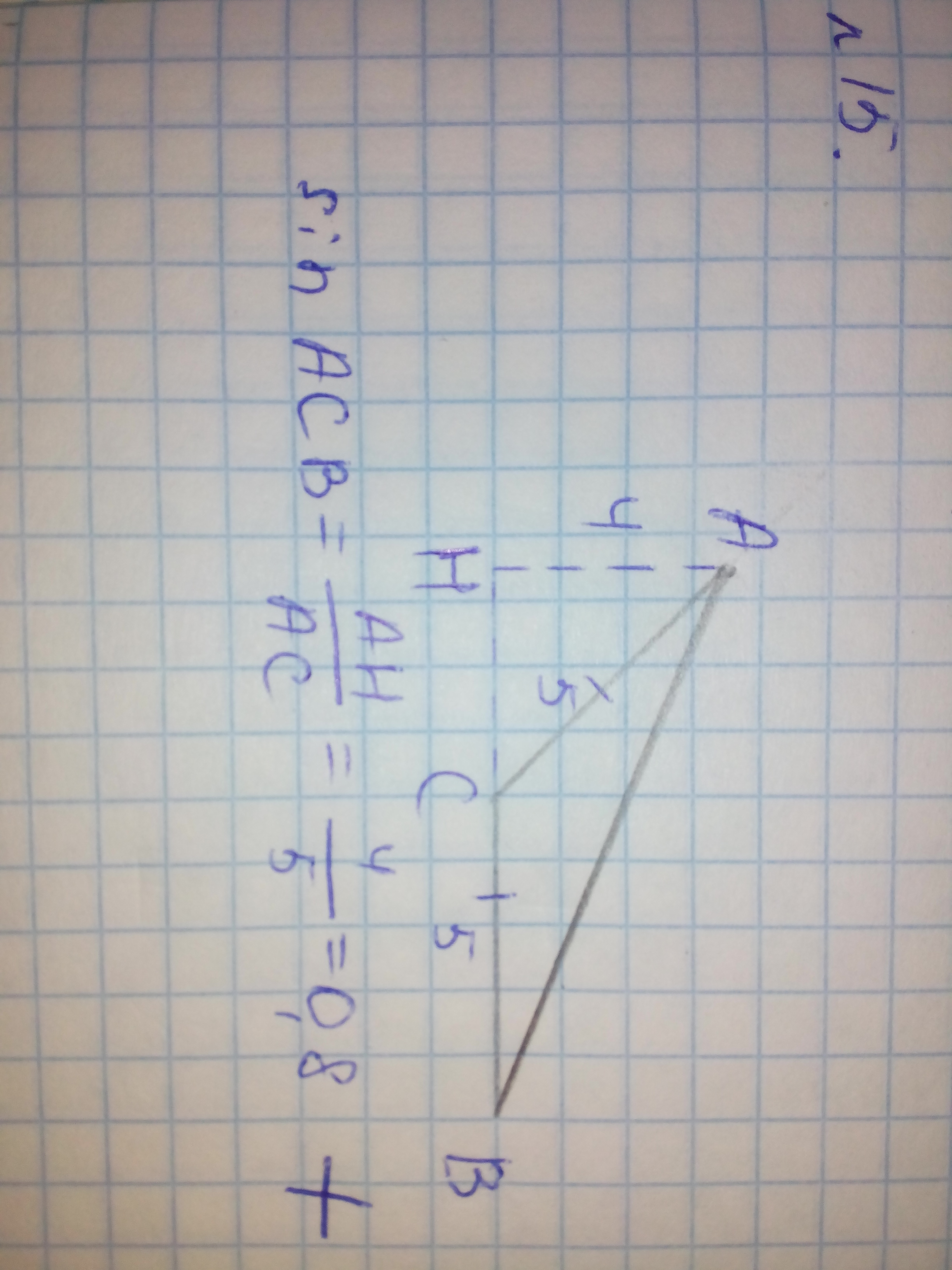Задача 2307 В тупоугольном треугольнике ABC AC=BC=5,...

slava191

24.11.2014

В тупоугольном треугольнике ABC AC=BC=5, высота AH равна 4. Найдите sin ACB.

HB=sqrt(5^2-4^2)=3
HC=3+5=8
AC=sqrt(8^2+4^2)=sqrt(80)
sin ACB = AH/AC = 4/sqrt(80)

P.S. Здесь я решил неправильно, если сможете решить нормально, плиз напишите как Предложить решение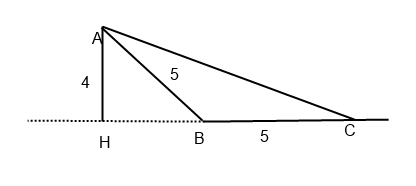

Ответ: 4/sqrt(80)

Гость

27.02.2015

1)Ищем сторону СН (в треугольнике АСН эта сторона является катетом). Согласно теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Поэтому:
АС^2=АН^2+СН^2 (^-степень)
СН^2=АС^2-AH^2
СН=√АС^2-AH^2, то есть:
СН=√5^2-4^2=√25-16=√9=3
Итак sinACB (отношение противолежащего катета к гипотенузе) равен:
sinACB=AH/AC
sinACB=4/5=0,8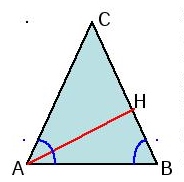

Гость

30.03.2015

По свойсву смежных углов: sinACB=sinACH.
Найдем sinACH: AH/AC=4/5=0,8

AnastasiyaHudyakova

29.04.2016

sin ACH=sin ACB
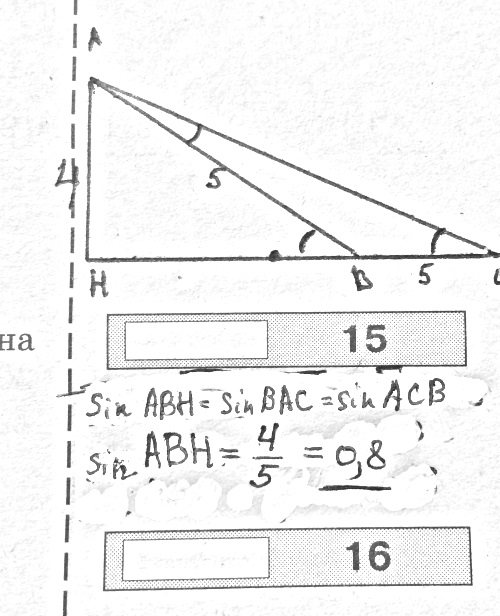
sin=4/5=0,8