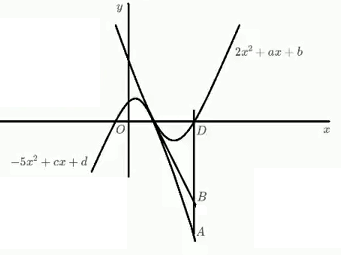
Задача 22644 Две параболы y=2x^2+ax+b и y=-5x^2+cx+d...

Kadridin11

19.01.2018

Две параболы y=2x^2+ax+b и y=-5x^2+cx+d касаются в точке, лежащей на оси Ox. Через точку D – вторую точку пересечения первой параболы с осью Ox – проведена вертикальная прямая, пересекающая вторую параболу в точке A, а общую касательную к параболам – в точке B. Найдите отношение DA:DB. 

SOVA

19.01.2018

★

По условию парабола у=2x^2+ax+b пересекает ось Ох дважды, т.е квадратное уравнение 2x^2+ax+b=0 имеет два корня
х_(о) и х_(D)
2x^2_(o)+ax_(o) +b=0
2х^2_(D)+ax_(D)+b=0
вычтем
2(x^2_(o)-x^2_(D))+а*(x_(o)-x_(D))=0
((x_(o)-x_(D))*(2x_(o)+2x_(D)+а)=0
x_(o)-x_(D)≠0, точки по условию различны.
Значит
2x_(o)+2x_(D)+а=0
(x_(o)+x_(D))=-a/2 (# 1)

точка касания расположена на оси Ox, значит (x_(o);0)

Составим уравнение касательной к параболе у=2x^2+ax+b.

f(x)=2x^2+ax+b
f(x_(o))=0,
f`(x)=4x+a
f`(x_(o))=4x_(o)+a

y-0=(4х_(о)+a)*(x-x_(o)) - уравнение касательной к первой параболе.


Составим уравнение касательной к параболе у=2x^2+ax+b.

f(x)=-5x^2+сx+d
f(x_(o))=0,
f`(x)=-10x+c
f`(x_(o))=-10x_(o)+c

y-0=(-10х_(о)+c)*(x-x_(o)) - уравнение касательной ко второй параболе.

Касательная общая, значит
4х_(о)+a=-10х_(о)+c ( угловые коэффициенты равны)
14x_(o) + a - c =0
x_(o)=(c-a)/14 ( # 2)

У точек А;В и D - одинаковые абсциссы.
Найдем ординаты.
Точка А лежит на второй параболе
Точка В на касательной

А(x_(D);-5x^2_(D)+cx_(D)+d)
В(х_(D);(4х_(о)+a)(x_(D)-x_(o))
D(х_(D); 0)

|AD|=|-5x^2_(D)+cx_(D)+d|
-5x^2_(o)+сx_(o) +d=0
d=5x^2_(o)-сx_(o)
|AD|=|-5x^2_(D)+cx_(D)+5x^2_(o)-сx_(o)|=
=|x_(o)-x_(D)|*|5x_(o)+5x_(D)-c|

|ВD|=|x_(o)-x_(D)|*|4x_(o)+a|

|DА|:|DВ|=|5x_(o)+5x_(D)-c|/|4x_(o)+a|
так как
(x_(o)+x_(D))=-a/2 ( # 1)
x_(o)=(c-a)/14 ( # 2)

|DА|:|DВ|=|5x_(o)+5x_(D)-c|/|4x_(o)+a|=

=|5*(-a/2)-c|/|(4*(c-a)/14)+a|=

=|(-5a-2c)/2|/|(2c+5a)/7|=7/2

О т в е т. 7/2