Задача 22563 Cosx=cos2x*cos3x...
Условие
предмет не задан
2271
Решение
★
cos альфа *cos бета =(1/2)*(cos( альфа + бета )+cos( альфа - бета ))
cosx=(1/2)cos5x+(1/2)cosx
(1/2)*(cos5x-cosx)=0
Формула
cos альфа -cos бета=-2* sin(( альфа + бета )/2)*sin(( альфа - бета )/2)
sin3x*sin2x=0
3x=Pik, k ∈ Z или 2х=Pin, n ∈ Z
x=(Pi/3)k, k ∈ Z или х=(Pi/2)*n, n ∈ Z
О т в е т. (Pi/3)k; (Pi/2)*n, k, n ∈ Z
Можно записать ответ иначе, с учетом того, что некоторые корни повторяются дважды
О т в е т. (Pi/3)k; (Pi/2)+(Pi)*n, k, n ∈ Z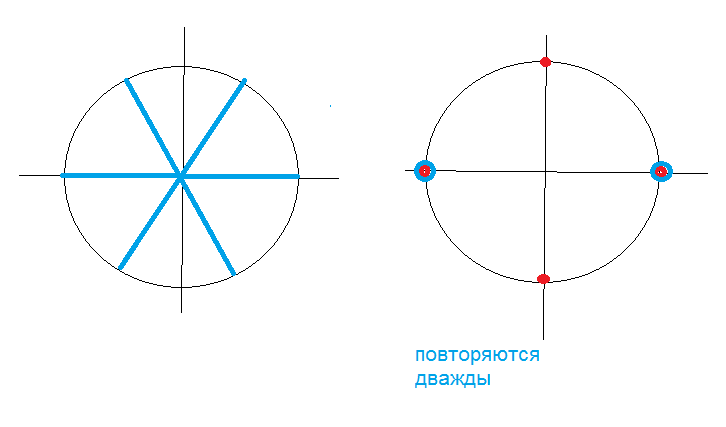
Все решения
cosx=cos2x*cos3x
cos2x*cos3x=1/2(cosx+cos5x);
cosx-1/2(cosx)-1/2(cos5x)=0;
1/2(cosx)-1/2(cos5x)=0; cosx-cos5x=sin3x*sin2x=0
sin3x=0. отсюда 3x=Pik. x=Pik/3,k ∈ z 2) sin2x=0. x=Pik/2
Ответ:Piк/3, Piк/2
