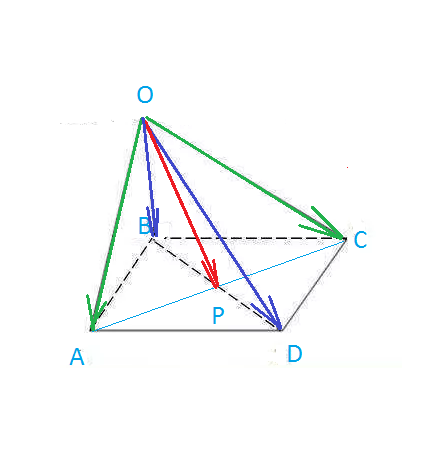
Задача 22485 1. Дан параллелограмм ABCD. Доказать,...

slava191

16.01.2018

1. Дан параллелограмм ABCD. Доказать, что vector{OA}+vector{ОС} = vector{ОВ}+vector{OD}, где О — произвольная точка пространства.

SOVA

16.01.2018

★

Пусть Р- точка пересечения диагоналей параллелограмма АВСD.

По правилу параллелограмма сложения векторов
vector{OA}+vector{OC}=2*vector{OP}

vector{OВ}+vector{OD}=2*vector{OP}
Значит

vector{OA}+vector{OC}=vector{OВ}+vector{OD}
vector{OD}=vector{OA}+vector{OC}-vector{OВ}