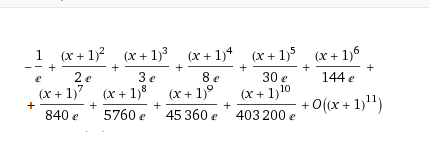Задача 22402 Разложить по формуле Тейлора функцию...

slava191

15.01.2018

Разложить по формуле Тейлора функцию f(x) в точке x0:

1) f(x)=xe^(x), x0=-1
2) f(x)=ln(2x-1), x0=1

SOVA

15.01.2018

1) можно использовать стандартные разложения с помощью замены переменной
x+1=t
Если х→-1, то t→0
f(x)=x*e^x или
f(t)=(t-1)*e^(t-1)
Разложим функцию f(t) по степеням t, используя разложение
e^t=1+t+(t^2/2!)+(t^3/3!)+(t^4/4!)+(t^5/5!) + o(t^5)
o(t^5) - остаточный член формулы Тейлора в форме Пеано

(t-1)*e^(t-1)=(1/e)*t*e^(t)-(1/e)*e^t

(1/e)*t*e^(t)=(1/e)*(t+t^2+(t^3/2!)+(t^4/3!)+(t^5/4!)+ о(t^5))
-(1/e)*e^t=(1/e)*(-1-t-(t^2/2!)-(t^3/3!)-(t^4/4!)-(t^5/5!) + o(t^5))
Cкладываем:

f(t)=(1/e)*(-1+(t^2/2)+(t^3/3)+(t^4/8)+(t^5/30)+o(t^5))

Обратная замена

x*e^x=(1/e)*(-1+((x+1)^2/2)+((x+1)^3/3)+((x+1)^4/8)+((x+1)^5/30)+o((x+1)^5))

сравнить ответ с ответом, полученным с помощью машинного разложения.