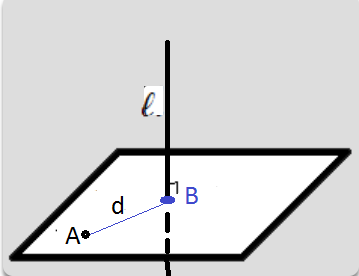
Задача 22352 5. Найти расстояние оси точки A(0; 2; 5)...

slava191

14 января 2018 г.

5. Найти расстояние оси точки A(0; 2; 5) до прямой (x–1)/(–2)=y/1=(z+3)/3

SOVA

14 января 2018 г.

★

Составим уравнение плоскости, проходящей через точку А, нормальный вектор которой совпадает с направляющим вектором данной прямой
–2·(х–0)+(у–2)+3·(z–5)=0
–2x+y+3z–17=0

Составим параметрические уравнения прямой
x–1=–2t; y=t; z+3=3t

x=–2t+1;
y=t;
z=3t–3

Подставляем х; у; z выраженные через t в уравнение плоскости.
–2·(–2t+1)+t+3·(3t–3)–17=0
14t–28=0
t=2

значит
х=–2·2+1=–3
у=2
z=3·2–3=3

В(–3;2;3) – точка пересечения прямой и плоскости.
АВ=√(–3–0)²+(2–2)²+(3–5)²=√13
О т в е т. √13