Задача 22350 3. Составить уравнение касательной...
Условие
математика ВУЗ
24147
Решение
★
(2–1)2+(–1+2)2+(–3–2)2=27,
1+1+25=27 – верно.
R=√27=3√3
C(1;–2;2)– центр сферы.
Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.
Значит вектор СM – нормальный вектор касательной плоскости.
\СM =(2–1;–1–(–2);–3–2)=(1;1;–5)
Уравнение плоскости с нормальным вектором n=(a;b;c) и проходящей через точку Мо(xo;yo;zo) имеет вид
a·(x–xo)+b·(y–yo)+c·(z–zo)=0
1·(x–2)+1·(y+1)–5·(z+3)=0
x+y–5z–16=0
О т в е т. x+y–5z–16=0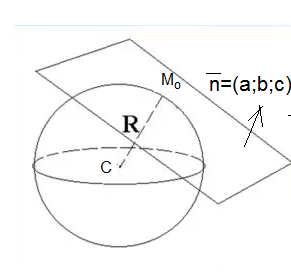
Обсуждения