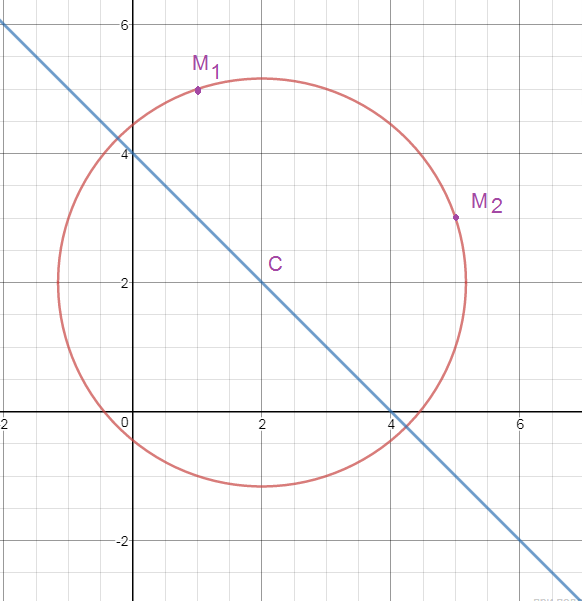
Задача 22146 4. Окружность проходит через точки...

slava191

09.01.2018

4. Окружность проходит через точки M1(1;5) и M2(5;3), а центр ее лежит на прямой x/4+y/4=1. Найти уравнение окружности.

SOVA

09.01.2018

★

Каноническое уравнение окружности с центром в точке С(a;b) имеет вид:
(x-a)^2+(y-b)^2=R^2

По условию
точка С лежит на прямой
(x/4)+(y/4)=1,
значит координаты точки С удовлетворяют этому уравнению
(a/4)+(b/4)=1
или
a+b=4

Окружность проходит через точки M1(1;5) и M2(5;3), значит координаты этих точек удовлетворяют уравнению окружности

Получили систему трех уравнений с тремя неизвестными
a, b, R
{a+b=4
{(1-a)^2+(5-b)^2=R^2
{(5-a)^2+(3-b)^2=R^2

Вычитаем из второго третье
(1-a)^2-(5-a)^2+(5-b)^2-(3-b)^2=0
Применяем формулу разности квадратов
(1-а-5+а)*(1-а+5-а)+(5-b-3+b)*(5-b+3-b)=0
-4*(6-2a)+2*(8-2b)=0
2a-b-2=0
Из первого выражаем b=4-a и подставляем в полученное уравнение
2a-(4-a)-2=0
3a-6=0
a=2
b=4-a=4-2=2

R^2=(1-2)^2+(5-2)^2
R^2=10

О т в е т. (x-2)^2+(y-2)^2=10