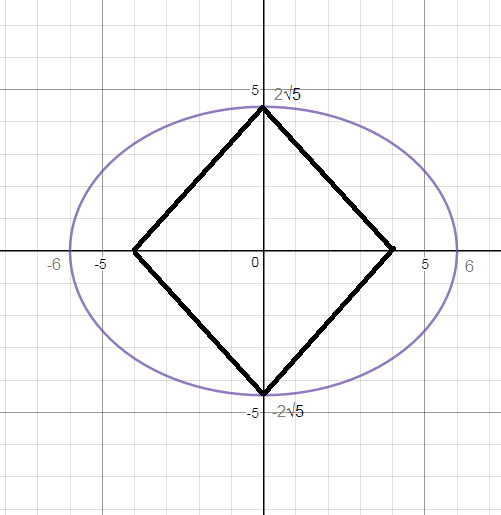
Задача 22107 4. Найти площадь четырехугольника, две...

slava191

08.01.2018

4. Найти площадь четырехугольника, две вершины которого лежат в фокусах эллипса 5x^2+9y^2-180=0, а две другие совпадают с концами его малой оси.

SOVA

08.01.2018

★

Запишем каноническое уравнение эллипса
(x^2)/(180/5)+(y^2)/(180/9)=1
или
(x^2)/(36)+(y^2)/(20)=1

a=6
b=sqrt(20)=2sqrt(5)
c^2=a^2-b^2=36-20=16

S(четырехугольника)=(1/2)d_(1)*d_(2)=(1/2)*8*4 sqrt(5)=

=16sqrt(5)

О т в е т. 16sqrt(5)