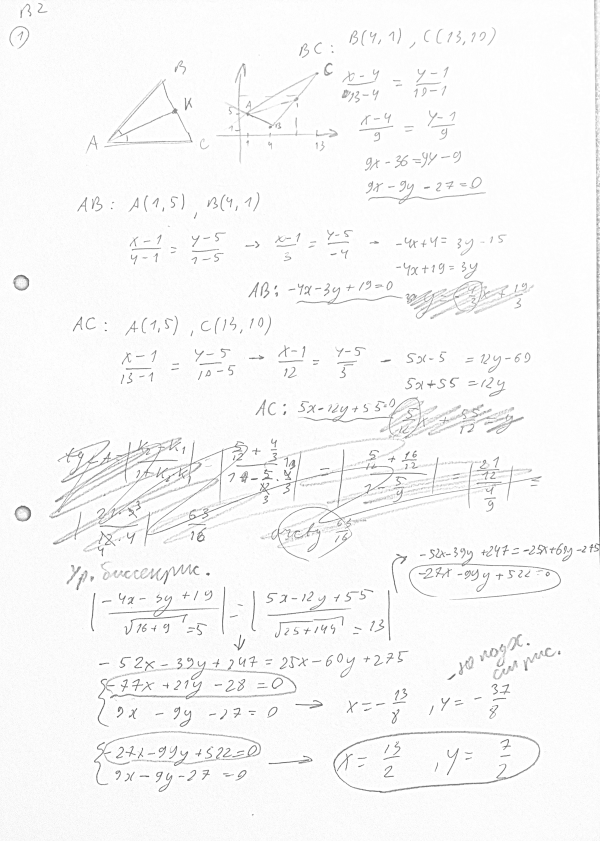Задача 22099 1) Дан треугольник ABC с вершинами...

slava191

08.01.2018

1) Дан треугольник ABC с вершинами А(1;5), B(4; 1), С(13; 10). Найти точку пересечения биссектрисы внутреннего угла А со стороной BC.

SOVA

08.01.2018

★

|АВ|=sqrt((4-1)^2+(1-5)^2)=sqrt(9+16)=sqrt(25)=5
|AC|=sqrt((13-1)^2+(10-5)^2)=sqrt(144+25)=sqrt(169)=13

Пусть АК - биссектриса, К ∈ BC.
Применяем свойство биссектрисы внутреннего угла треугольника.
Биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

ВК:КС=АВ:АС=5:13
Точка К делит отрезок ВС в отношении 5:13
лямбда =5/13
Применяем формулу нахождения координат точки, делящей отрезок в данном отношении
x_(K)=(x_(B)+ лямбда x_(C))/(1+ лямбда )
y_(K)=(y_(B)+ лямбда y_(C))/(1+ лямбда )

x_(K)=(4+(5/13)*13)/(1+(5/13))=13/2
y_(K)=(1+(5/13)*10)/(1+(5/13))=63/18=7/2

К(13/2; 7/2)

О т в е т. К(13/2; 7/2)

vk318474530

09.01.2018

Вариант решения через уравнение биссектрис.