Задача 21998 Решите неравенство...
Условие
lg(9y^2-3y+1)/lg(8y^2-6y+1)^3 < = log(5^3) 9 / log5 9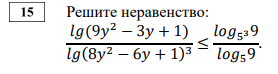
математика 10-11 класс
21272
Решение
★
log_(5^3)9=(1/3)log_(5)9
log_(c)a/log_(c)b=log_(b)a, a > 0, b > 0, b ≠ 1, c > 0 , c ≠ 1
Неравенство принимает вид:
log_(8y^2-6y+1)(9y^2-3y+1) меньше или равно 1
Метод рационализации позволяет заменить неравенство системой неравенств:
{9y^2-3y+1 > 0
{8y^2-6y+1 > 0 , 8y^2-6y+1 ≠ 1
{(8y^2-6y+1-1)*(9y^2-3y+1-8y^2+6y-1) меньше или равно 0
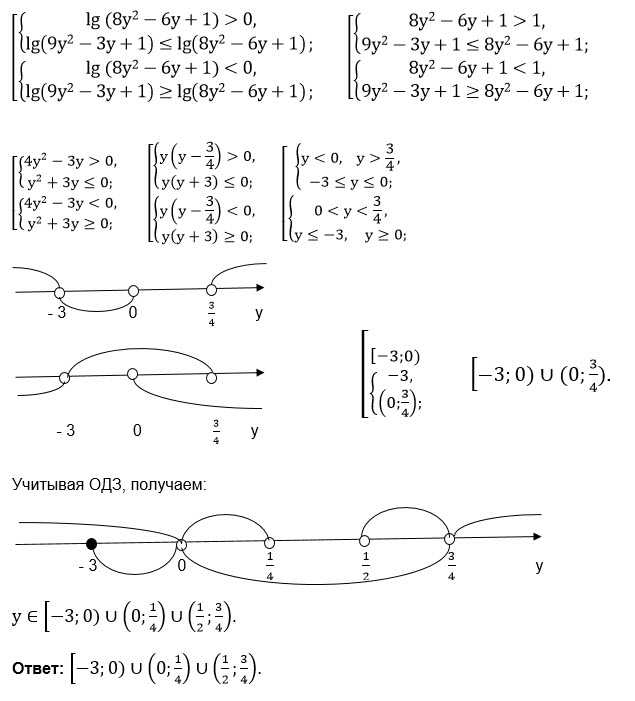
О т в е т. [-3;0)U(0;1/4)U(1/2;3/4)
Все решения