Условие
Дана правильная треугольная призма ABCA1B1C1, сторона основания которой равна 2, диагональ боковой грани sqrt(5). Найти угол между плоскостью A1BC и плоскостью основания призмы.
математика 10-11 класс
16885
Решение
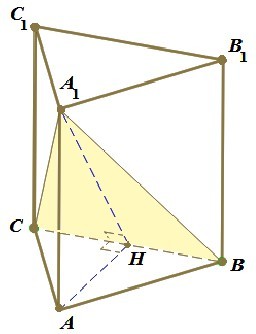
Обозначим середину ребра BC буквой H. Отрезки AH и A1H перпендикулярны BC, так как треугольник ABC - равносторонний, а A1BC - равнобедренный. Следовательно, угол A1HA - линейный угол двугранного угла с гранями BCA и BCA1.
Рассмотрим треугольник A1AB: по теореме Пифагора найдем AA1=1.
Рассмотрим треугольник AHB: по теореме Пифагора найдем AH=sqrt(5).
Из треугольника HAA1 находим: A1HA=AA1/AH=1/sqrt(3)
Отсюда находим: угол A1HA=30.
Ответ: 30
Вопросы к решению (1)
Почему ничего не понятно,где всё взялось и на каком основании,написано только что сделать и ответ,а само решение,где?
Вы не можете написать теорему Пифагора для треугольника и подставить в нее числа?
Написать комментарий
