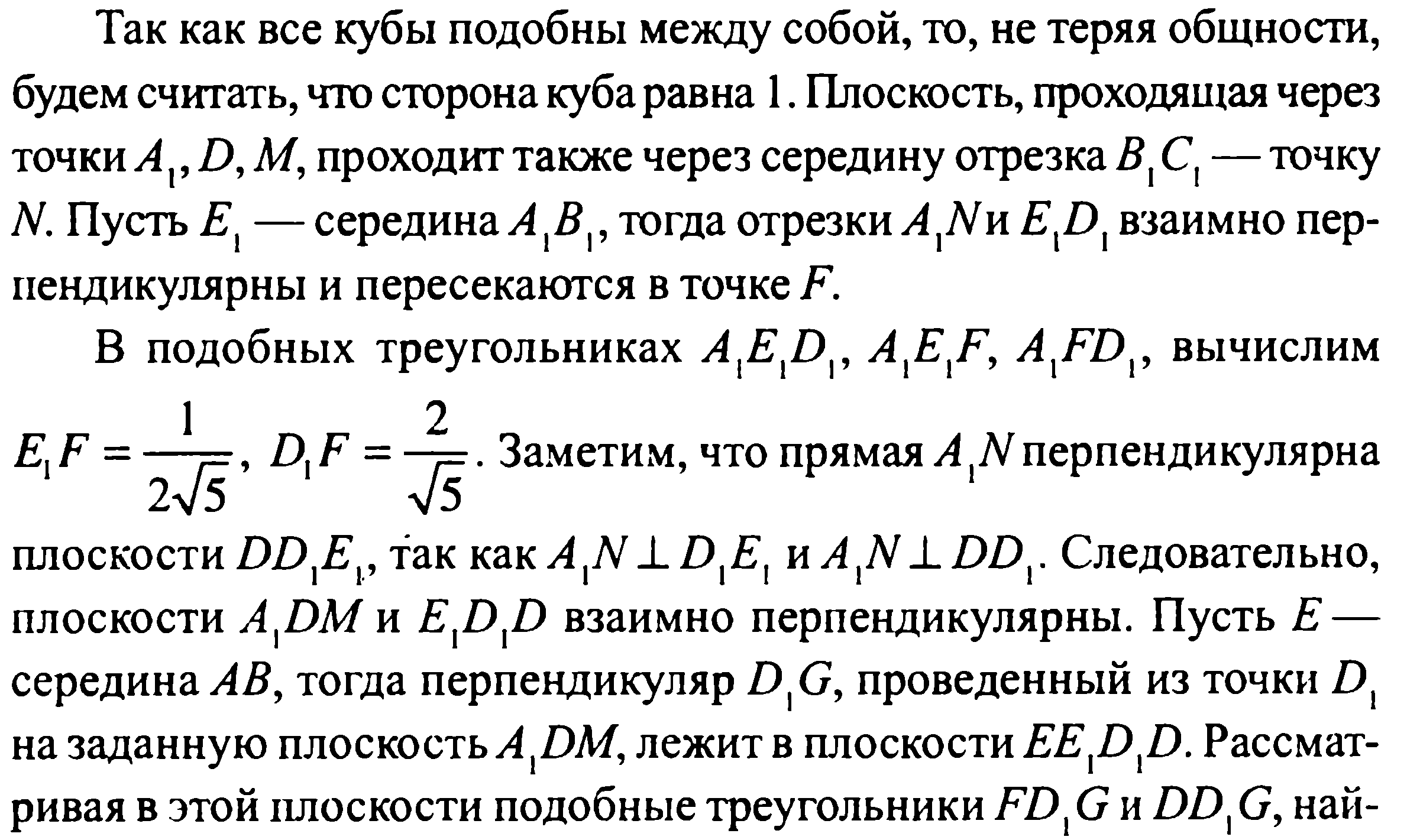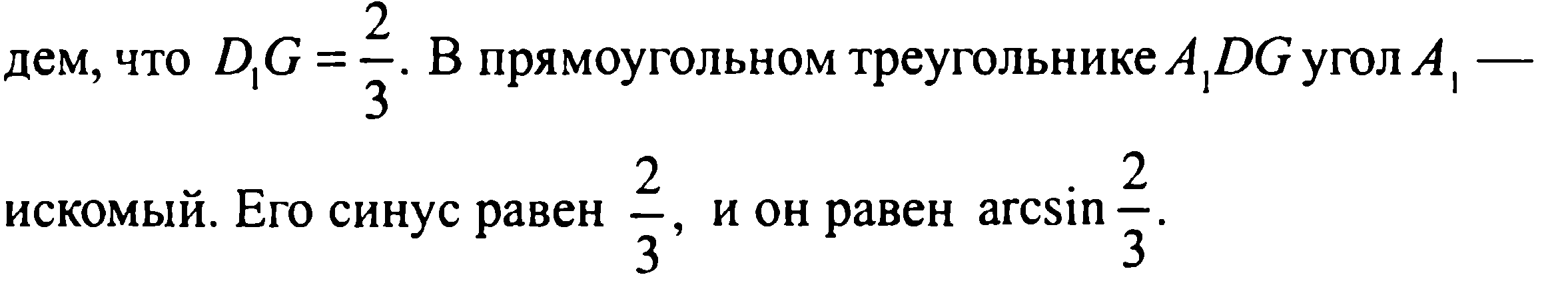Задача 218 В кубе ABCDA1B1C1D1 найдите угол между...
Условие
математика 10-11 класс
3023
Решение
Ответ: arcsin(2/3)
Все решения
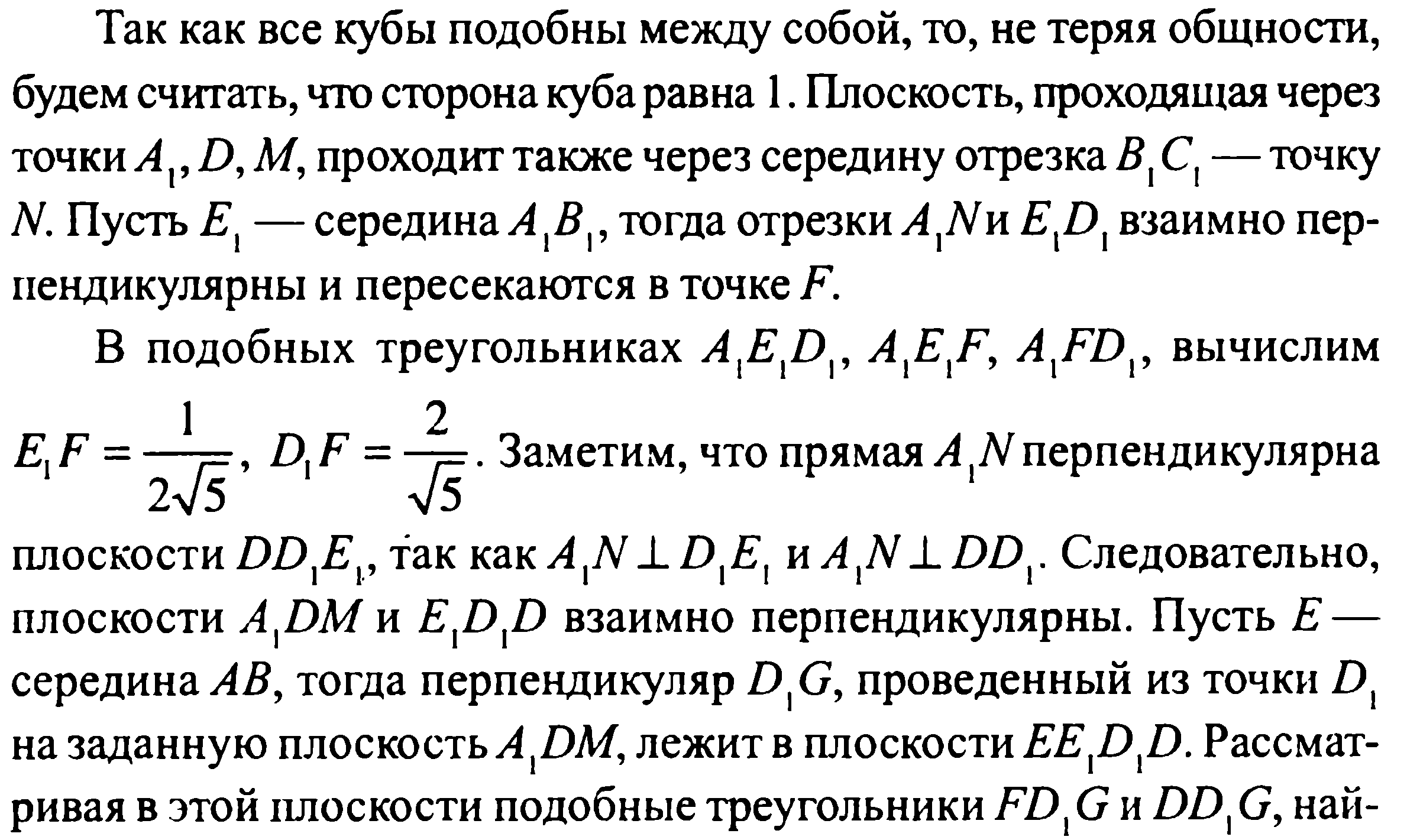
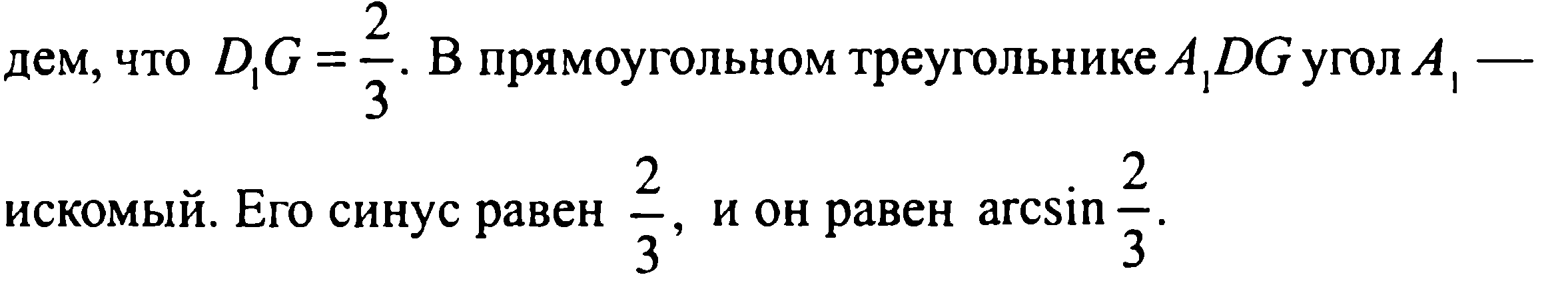
Ответ: arcsin(2/3)