Задача 216 В правильной треугольной пирамиде SABC с...

slava191

05.01.2014

В правильной треугольной пирамиде SABC с вершиной S сторона основания равна 12, а боковое ребро наклонено к основанию под углом, квадрат тангенса которого равен 0,5. Найдите расстояние между ребрами АВ и SC.

Искомое расстояние реализует общий перпендикуляр, соединяющий эти отрезки. В стереометрических задачах мы стремимся отыскать ту плоскость, в которой разворачиваются главные события сюжета задачи.

Пусть D — середина отрезка АВ. Рассмотрим плоскость SCD, в ней развернутся главные события в решении задачи. Прямая АВ перпендикулярна SCD, т. к. она перпендикулярна двум прямым SD и CD этой плоскости. Следовательно, высота DH в треугольнике SCD является тем самым общим перпендикуляром, длину которого нам надо найти. Зная тангенс угла, вычислим sin SCD =1/sqrt(3), и отсюда найдем DH = CD • sinSCD =12*sqrt(3)/2*1/sqrt(3)= 6.


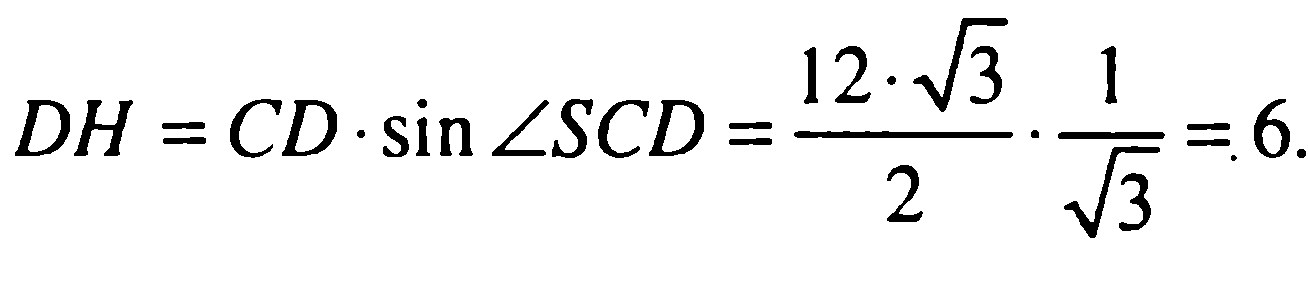
Ответ: 6