Задача 21531 Число 49 представлено в виде

РЕШЕНИЕ ОТ SOVA ✪ ЛУЧШЕЕ РЕШЕНИЕ

Пусть числа х и у.
x > 0; y > 0
По условию
49=x*y ⇒ y=49/x
Сумма чисел
x+y=x+(49/x)
Обозначим сумму чисел
f(x)=x+(49/x)
Исследуем функцию f(x) на экстремум.
f`(x)=1-(49/x^2)
f`(x)=0
x^2-49=0
x=-7 ( не удовл. усл. x > 0) или х=7
Исследуем точку х=7 на экстремум.
Находим знак производной
_-__ (7) _+__

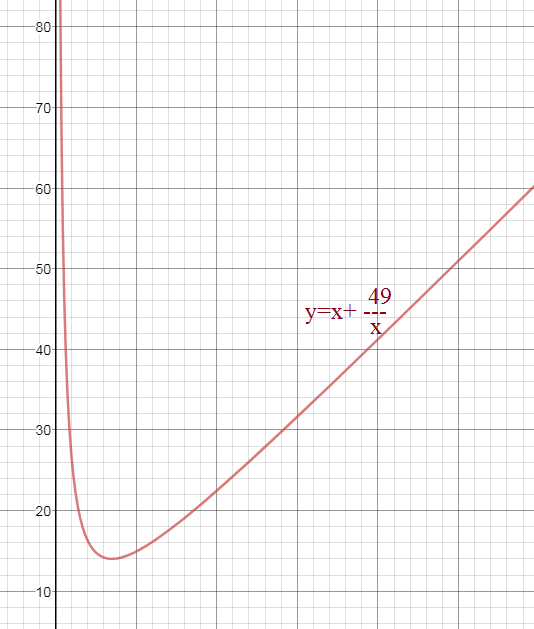
x=7 - точка минимума функции, значит при х=7 сумма чисел наименьшая.
Если х=7, то y=49/7=7

График функции у=х+(49/х) см. на рисунке.

[b]В условии задачи не сказано, что числа натуральные.[/b]

Поэтому наибольшим может быть любое число,

Например 98 * (1/2)
и т.д.
98+(1/2)=98,5

Если речь идет о наименьшей сумме, то ответ 7

Войдите и расскажите всем об этом!

Зарегистрируйся и спрашивай!

РЕШЕНИЕ ОТ u859314469

Число 49 может быть представлено в виде произведения как 7х7 или 49х1. В первом случае сумма =14, во втором =50 . Следовательно, наибольший сомножитель 49. Вопросы и комментарии 495-720-0951 или prois@mail.ru Елена Викторовна

Войдите и расскажите всем об этом!

Зарегистрируйся и спрашивай!