Задача 21528 Длина стороны основания правильной...

slava191

21.12.2017

Длина стороны основания правильной треугольной пирамиды равна 1, а площадь боковой поверхности пирамиды равна sqrt(3)/2 . Найдите длину высоты пирамиды.

SOVA

21.12.2017

★

L- апофема пирамиды
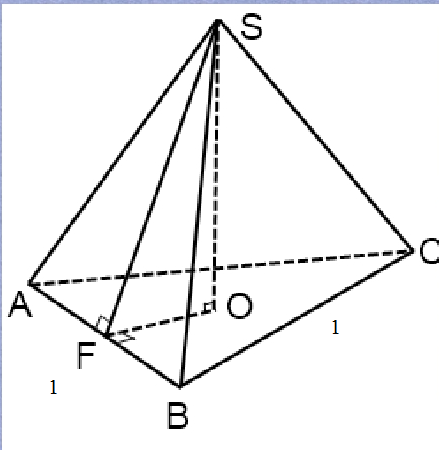
L=SF
S(бок)=(1/2)P(осн.)*L
sqrt(3)/2=(1/2)*3*L
L=sqrt(3)/3

OF=r=asqrt(3)/6=sqrt(3)/6

По теореме Пифагора из треугольника SOF

SO^2=SF^2-OF^2=(sqrt(3)/3)^2-(sqrt(3)/6)^2=

=(3/9)-(3/36)=1/4

SO=1/2