Задача 21525 а) Решите уравнение...
Условие
cos^23x-2cos3xsin(x-Pi/6)+1=0
б) Найдите решения уравнения, принадлежащие промежутку [2016Pi; 2017Pi]
Решение
сos3x=a
sin(x-(Pi/6))=b
Уравнение имеет вид
a^2-2ab+1=0
[b]Значит надо выделить полный квадрат(!) [/b]
(сos3x-sin(x–(π/6))^2-sin^2(x–(π/6))+1=0
Так как
1-sin^2(x–(π/6))=cos^2(x-(π/6))
уравнение принимает вид
(сos3x-sin(x–(π/6))^2+cos^2(x-(π/6))=0
Сумма квадратов равна 0, когда каждый 0.
Система уравнений
{cos3x-sin(x-(Pi/6))=0
{cos(x-(Pi/6))=0
Решаем первое уравнение
cos3x-sin(x-(Pi/6))=0
По формулам приведения
sinальфа =cos((Pi/2)- альфа)
сos3x-cos((Pi/2)-x+(Pi/6))=0
cos3x-cos((2Pi/3)-x)=0
Применяем формулу разности косинусов
-2sin(x+(Pi/3))*sin(2x-(Pi/3))=0
sin(x+(Pi/3))=0 или sin(2x-(Pi/3))=0
x+(Pi/3)=Pik, k ∈ Z или 2x-(Pi/3))=Pin, n ∈ Z
x=(-Pi/3)+Pik, k ∈ Z или х=(Pi/6)+(Pi/2)n, n ∈ Z
Решаем второе уравнение
cos(x-(Pi/6))=0
x-(Pi/6)=(Pi/2)+Pim, m ∈ Z
x=(2Pi/3)+Pim, m ∈ Z
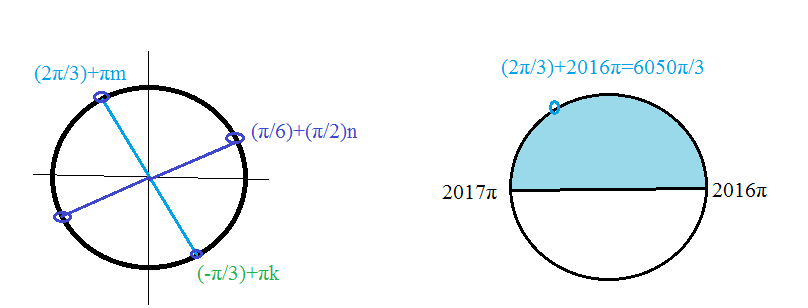
{x=(-Pi/3)+Pik, k ∈ Z или х=(Pi/6)+(Pi/2)n, n ∈ Z
{x=(2Pi/3)+Pim, m ∈ Z
О т в е т.
а)(-Pi/3)+Pik, k ∈ Z
б) Указанному промежутку принадлежит
х=(-Pi/3)+Pi*2017=6050Pi/3