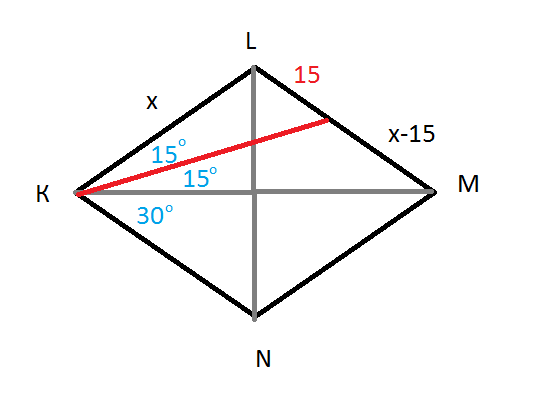
Задача 21431 В ромбе KLMN KS – биссектриса угла MKL,...

u178173117137

20.12.2017

В ромбе KLMN KS – биссектриса угла MKL, угол LKN равен 60°, LS = 15 см. Найдите площадь ромба KLMN.

SOVA

20.12.2017

★

Диагонали ромба являются биссектрисами его углов.
Поэтому ∠ NKL=60 градусов, ∠ KLM = 120 градусов.
Пусть сторона ромба равна х,
SM=x-15
КМ=xsqrt(3) по теореме косинусов из треугольника KLM

Биссектриса угла КS сторону LM на отрезки, пропорциональные прилежащим сторонам треугольника.
LS : SM=KL: KM
x: 15= xsqrt(3) : (x-15)
15sqrt(3)=x-15
x=15*(sqrt(3)+1)

S ( ромба)=x^2*sin60 градусов=225*(3+2sqrt(3)+1)*sqrt(3)/2=

=225*(2sqrt(3)+3)

О т в е т. 225*(2sqrt(3)+3)