Задача 21392 В равнобедренном прямоугольном...
Условие
Решение
vector{n}=(6;4)
Нормальные векторы взаимно перпендикулярных прямых ортогональны.
Значит нормальный вектор прямой, перпендикулярной данной имеет координаты
(2;–3)
Скалярное произведение 6•2+4•(–3)=0–верно
Уравнение перпендикулярной прямой имеет вид
2х–3у+с=0
Подставим координаты точки (5;7)
2•5–3•7+с=0
с=11
2х–3у+11=0 – уравнение второго катета.
Треугольник равнобедренный прямоугольный. Значит прямая, задающая гипотенузу, образует угол 45 градусов с каждым катетом.
Значит и нормальные векторы гипотенузы и катета образуют между собой угол 45 градусов.
Угол между вектором vector{n}=(6,4) и нормальным вектором гипотенузы обозначим координаты m и k, равен 45 градусов.
cos45 градусов=(6m+4k)/sqrt(6^2+4^2)*sqrt(m^2+k^2)
sqrt(2)/2=(6m+4k)/sqrt(6^2+4^2)*sqrt(m^2+k^2)
26(m^2+k^2)=36m^2+48mk+16k^2)
5m^2+24mk-5k^2=0
D=24^2-4*5*(-5)=576+100=676
m=1/5k или m=-5k
(1/5)kx+ky+d=0
(1/5)x+y+(d/k)=0
Подставлям координаты точки А
(1/5)*5+7+(d/k)=0
d/k=-8
(1/5)x+y-8=0
x+5y-40=0 - уравнение прямой, проходящей через точку А и образующей угол 45 градусов с катетом 6х+4у-9=0
или
-5kx+ky+p=0
-5x+y+(p/k)=0
Подставляем координаты точки А
-25+7+(p/k)=0
p/k=18
-5x+y+18=0 или 5х-y-18=0
О т в е т.
2х–3у+11=0
5х-у-32=0
или
2х–3у+11=0
х+5у-40=0
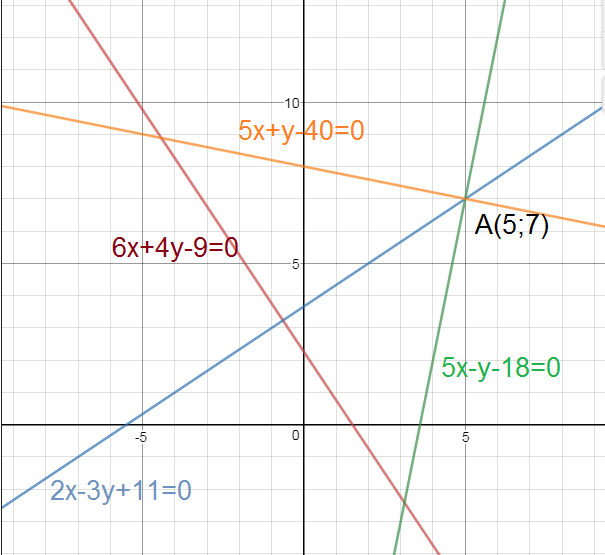
(см. рис. зеленая или оранжевая прямая гипотенуза)