Задача 21375 log2(2x^2+x-3)+log2(x^2-x-3) > =...
Условие
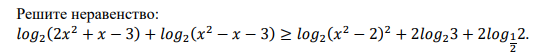
Решение
{2x^2+x-3 > 0 x∈(-∞;-3/2)U(1:+∞)
{x^2-x-3 > 0 x∈(-∞;(1-sqrt(13))/2)U((1+sqrt(13))/2;+∞)
{(x^2-2)^2 > 0 x∈(-∞;-sqrt(2))U(-sqrt(2);sqrt(2))U(sqrt(2);+∞)
ОДЗ x∈(-∞;(1-sqrt(13))/2)U((1+sqrt(13))/2;+∞)
log_(2)(2x^2+x-3)+log_(2)(x^2-x-3)=log_(2)(2x^2+x-3)(x^2-x-3)
2log_(2)3=log_(2)3^2=log_(2)9
2log_(1/2)2=log_(1/2)2^2=log_(1/2)4=-log_(2)4
log_(2)(x^2-2)^2+2log_(2)3-log_(2)4=log_(2)(9(x^2-2)^2/4)
log_(2)(2x^2+x-3)(x^2-x-3) больше или равно log_(2)(9(x^2-2)^2/4)
Логарифмическая функция с основанием 2 возрастающая, поэтому
(2x^2+x-3)(x^2-x-3) больше или равно 9(x^2-2)^2/4
x^2*(x^2+4x+4) меньше или равно 0
x=0 или x^2+4x+4=0 х=-2
C учетом ОДЗ получаем ответ.
х=-2
О т в е т. -2