Задача 21296 Постройте график функции y=(( x^2+...
Условие
Решение
-1-х ≠ 0
х ≠ - 1
-1-x=-(1+x)
Сокращаем на (х+1) и числитель и знаменатель.
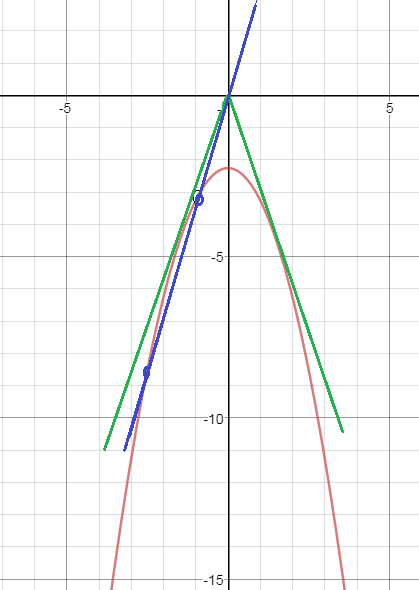
Строим параболу у=-(x^2+2,25)
на (- бесконечность;-1)U(-1;+ бесконечность)
При х=-1 получаем, что у=-((-1)^2+2,25)=-3,25
точка (-1;-3,25) не принадлежит графику функции
Прямая у=kx, проходящая через эту точку пересекает график в одной точке.
-3,25=-k⇒ k=3,25
Прямые у=kx, которые являются касательными тоже будут иметь одну общую точку с графиком.
Составим уравнения таких касательных в точке с абсциссой х_(о)
у_(о)=-х^2_(о)-2,25
Находим
f`(x)=-2x
f`(x_(o))=-2x_(o)
y-(х^2_(о)-2,25)=-2x_(o)*(x-x_(o))
Так как касательные проходят через начало координат, то
подствляем в это уравнение вместо х 0 и вместо у 0
х^2_(о)=2,25
x_(о)=-1,5 или x_(o)=1,5
y_(о)=-4,5 или y_(о)=-4,5
k=3 или k=-3
О т в е т. -3; 3; 3,25