Задача 21226 ...

slava191

17 декабря 2017 г.

Основанием пирамиды SABCD является параллелограмм ABCD. Точки K, L, M расположены на рёбрах SA, SB, SC соответственно, и при этом

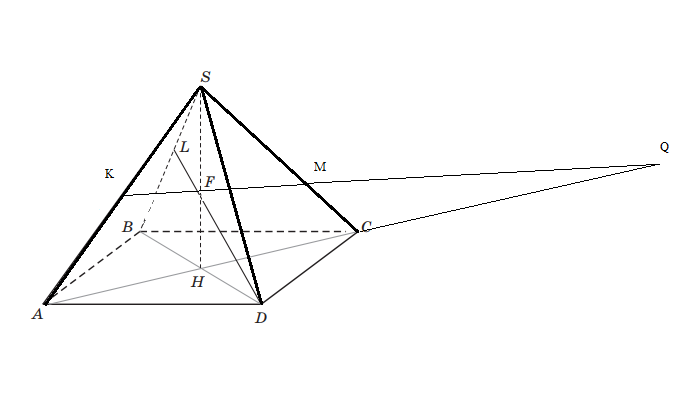
SK/SA = 1/2; SL/SB = 2/5; SM/SC = 2/3

а) Докажите, что прямые KM и LD пересекаются.

б) Найдите отношение объёма пирамиды SKLMD к объёму пирамиды SABCD.

SOVA

21 декабря 2017 г.

★

a) Пусть КМ пересекается с SH (высотой пирамиды) в точке F.
Q– точка пересечения KM c AC.
По теореме Менелая
(SK/KA)·(AQ/QC)·(CM/MS)=1
AQ=2QC
AC=CQ
так как диагонали параллелограмма в точке пересечения делятся пополам, то АН=НС=z
CQ=2z
По теореме Менелая для треугольника SHC и прямой КМ
(SF/FH)·(HQ/QC)·(CM/MS)=1
3SF=4FH
HF/FS=3/4

Пусть LF пересекается с BD в точке G
По теореме Менелая для треугольника SBH и пресекающей его прямой GF
(SL/LB)·(BG/GH)·(HF/FS)=1
(2/3)·(BG/GH)·(3/4)=1
(BG/GH)=2
BH=HG

Значит, G=D

б)
Объемы двух треугольных пирамид, имеющих по равному трехгранному углу, относятся друг к другу, как произведения длин трех ребер равных трехгранных углов''.

Пирамиды SKLM и SABC имеют общий трехгранный угол.
Поэтому
V(SKLM)/V(SABC)=(SK/SA)·(SL/SB)·(SM/SC)
V(SKLM)/V(SABC)=(1/2)·(2/5)·(2/3)=2/15

V(SKLM)/V(SABC)=2/15
V(SABC)=(1/2)V(SABCD)

V(SKLM)=(1/15)V(SABCD)

Аналогично,
V(SKMD)/V(SACD)=(SK/SA)·(SM/SC)·(SD/SD)=(1/2)·(2/3)=(1/3)
V(SKMD)=(1/3)V(SACD)=(1/6) V(SABCD)

V(SKLMD)=V(SKLM)+V(SKMD)=((1/15)+(1/6))V(SABCD)=
=(7/30)V(SABCD)

О т в е т.
б) V(SKLMD):V(SABCD) =7:30