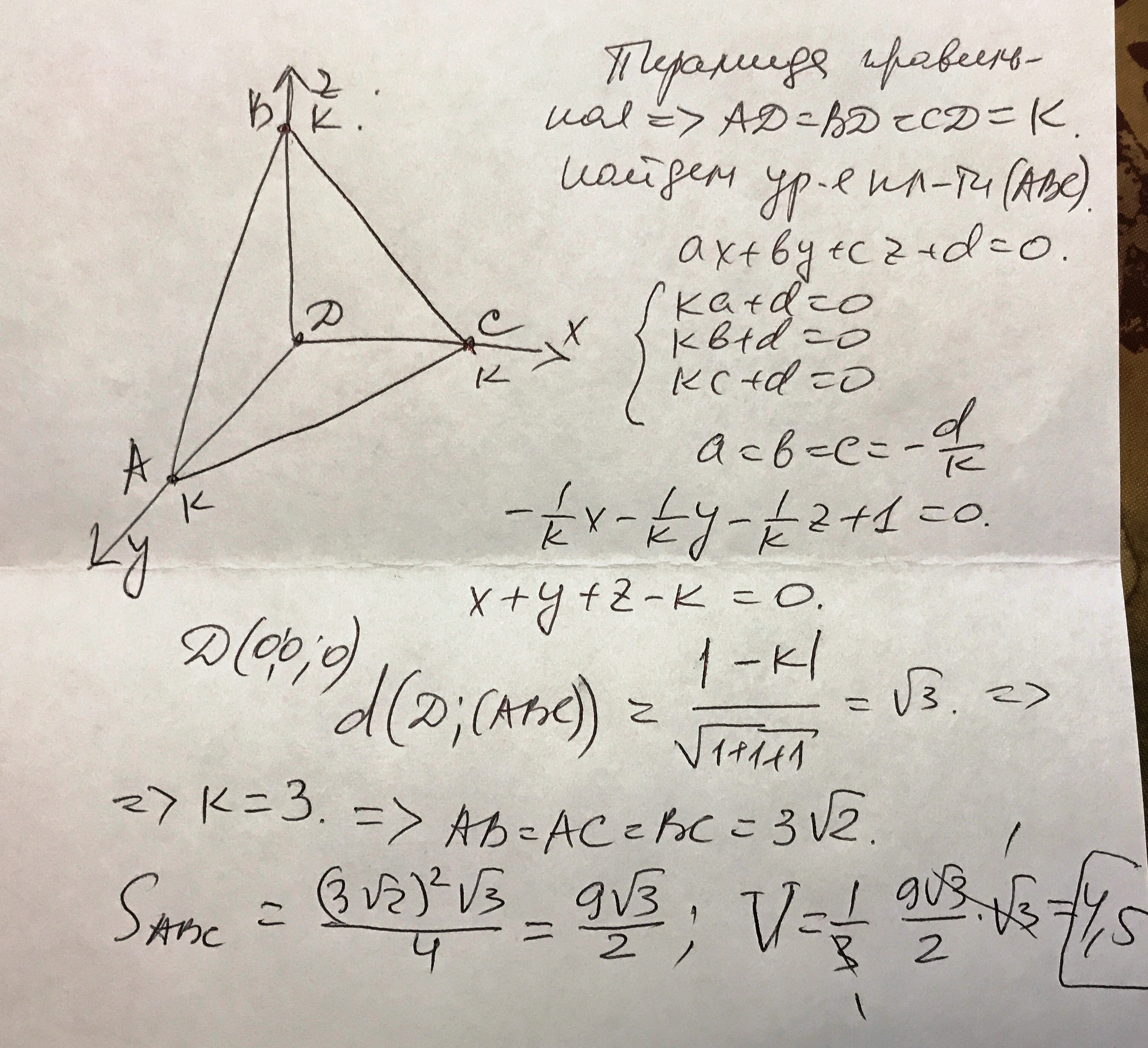Задача 21207 ...

slava191

17.12.2017

Длина высоты правильной треугольной пирамиды равна sqrt(3), а все плоские углы при вершине пирамиды — прямые. Найдите объём пирамиды.

SOVA

17.12.2017

★

Пусть сторона основания равна а.
Тогда S(осн.)=a^2sqrt(3)/4
Боковые ребра пирамиды- катеты прямоугольных треугольников с гипотенузой а.
Значит, боковые ребра пирамиды равны (a*sqrt(2))/2
Высота пирамиды проектируется в центр правильного треугольника ( это центр как вписанной, так и описанной окружности).
Радиус описанной окружности
R=(a*sqrt(3))/3
По теореме Пифагора
H^2=(asqrt(2)/2)^2-(asqrt(3)/3)^2

H=sqrt(3)
3=(a^2/2)-(a^2/3)
a^2=18
a=3sqrt(2)
V=(1/3)S*H=(1/3)a^2sqrt(3)/4*(sqrt(3))=(1/3)*18*(3)/4=4,5

u859314469

17.12.2017

Вопросы и комментарии 495-720-0951 или prois@mail.ru Елена Викторовна