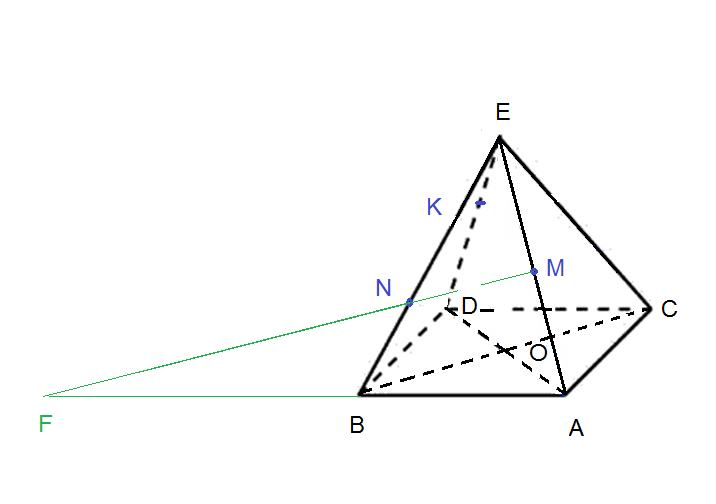
Задача 21171 На боковых ребрах ЕА, ЕВ, ЕС правильной...
Условие
а) Постройте сечение пирамиды плоскостью, проходящей через точки М, N, К
б) В каком отношении плоскость (MNK) делит объем пирамиды?
Решение
Все ребра пирамиды равны.
Вершина Е проектируется в центр квадрата- точку пересечения диагоналей ( точку О).
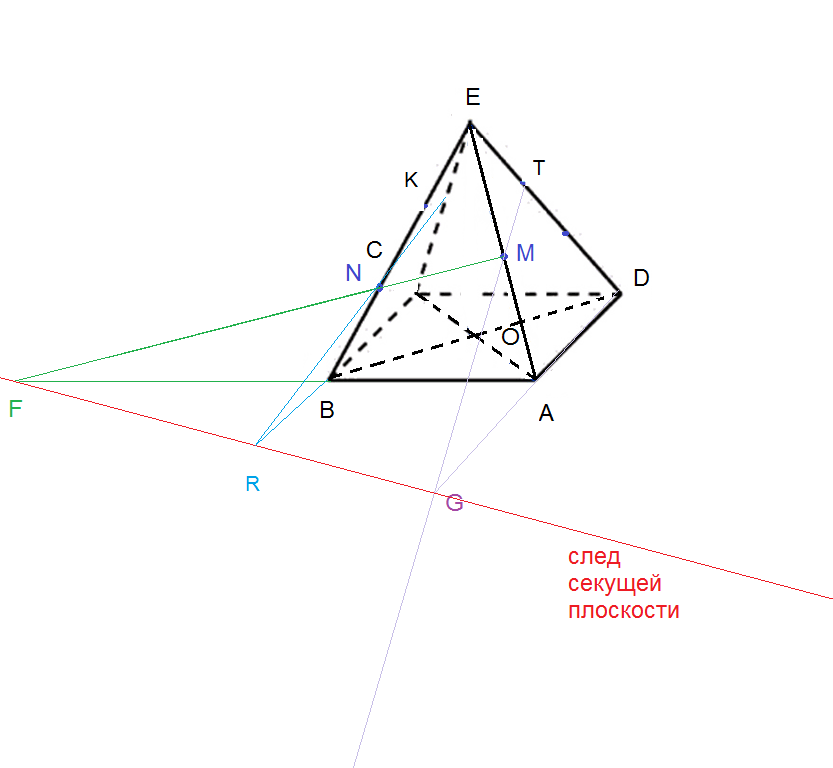
Построение сечения.
Соединяем М с N и продолжаем до пересечения с АВ.
Получаем точку F.
Соединяем K с N и продолжаем до пересечения с CB.
Получаем точку R.
Прямая FR - след секущей плоскости на основании АВСD
Продолжаем DB до пересечения с FR. Получаем точку Q.
Соединяем точку Q с точкой N и продолжаем до пересечения с ребром ЕD.
Получаем точку Т.
Сечение NKTM - искомое.
б)
Пирамиды ЕВСА и ЕNKM имеют общий трехгранный угол.
''Объемы двух треугольных пирамид, имеющих по равному трехгранному углу, относятся друг к другу, как произведения длин трех ребер равных трехгранных углов''.
Поэтому
V(ENKM)/V(EBCA)=(EM/EA)*(EN/EB)*(EK/EC)
V(ENKM)/V(EBCA)=(1/2)*(2/3)*(1/3)
V(ENKM)/V(EBCA)=1/9
V(EBCA)=(1/2)V(EABCD)
V(ENKM)=(1/18)V(EABCD)
Аналогично,
V(EMTK)/V(EACD)=(EM/EA)*(ET/ED)*(EK/EC)
Для нахождения отношения ET/ED применяем теорему Менелая.
По условию ЕМ : ЕА = 1:2, значит ЕМ:МА=1:1
EN : ЕВ = 2 :3, значит EN:NB=2:1
ЕК : ЕС = 1:3, значит EK:KC=1:2.
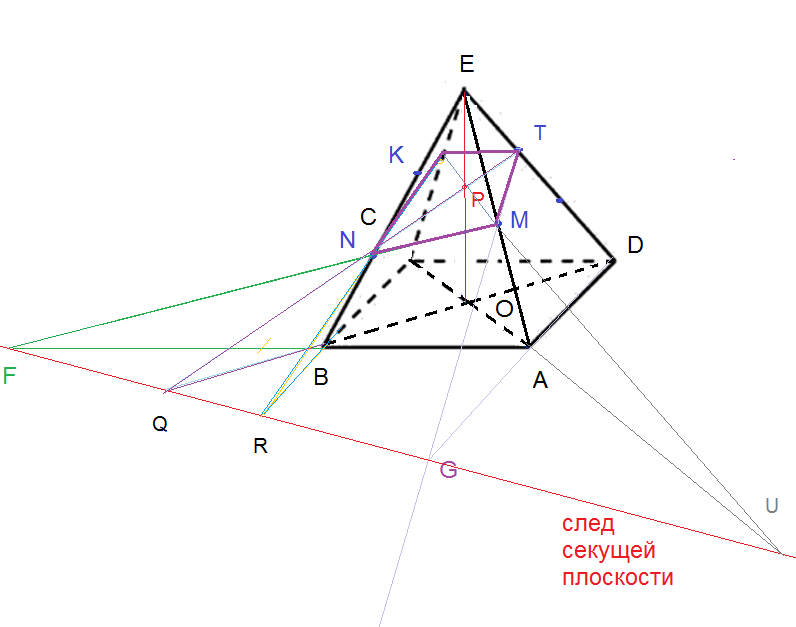
Из треугольника ЕСА
(ЕК/КС)*(СU/UA)*(AM/ME)=1 ⇒CA+AU=2AU; AU=CA
Из треугольника ЕОА
(EP/PO)*(OU/UA)*(AM/ME)=1
3EP=2PO
EP/PO=2/3
Треугольника BEO
(EN/NB)*(BQ/QO)*(OP/PE)=1
BQ/QO=1/3
BQ/QD=1/5
Из треугольника EBD
(EN/NB)*(BQ/QD)*(DT/TE)=1
TE/DT=2/5
ET/ED=2/7
V(EMTK)/V(EACD)=(EM/EA)*(ET/ED)*(EK/EC)=(1/2)*(2/7)*(1/3)=1/21
V(EMTK)=(1/15)V(EACD)=(=(1/42)V(EABCD)
V(EMNKT)=V(ENKM)+V(EMTK)=((1/18)+(1/42)) V(EABCD)=(5/63) V(EABCD)=(
V(EMNKT): V(EABCD)=5:58
О т в е т. 5:58
Все решения

