Задача 21164 В правильной четырехугольной пирамиде...

slava191

16.12.2017

В правильной четырехугольной пирамиде боковое ребро равняется 4 и образует с плоскостью основания угол 30°. Найдите объём пирамиды.

SOVA

16.12.2017

★

В основании пирамиды - квадрат.
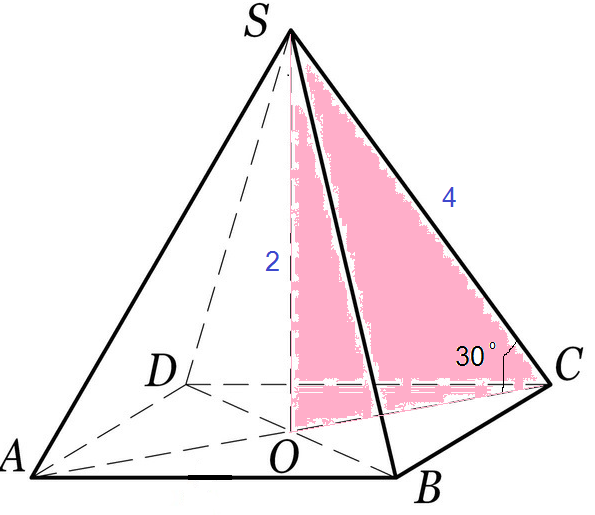
Высота проектируется в центр квадрата- точку О.
Точка О - точка пересечения диагоналей.
АО=ОВ=ОС=ОD.
Равные проекции имеют равные наклонные.
Все ребра пирамиды равны. Угол между боковым ребром и плоскостью основания - это угол между боковым ребром и его проекцией на основание.
Из прямоугольного треугольника SCO с острым углом в 30 градусов находим SO=2 ( катет против угла в 30 градусов равен половине гипотенузы)
По теореме Пифагора
ОС=sqrt(4^2-2^2)=sqrt(12)=2sqrt(3)
АС=4sqrt(3)
AD=AC*sin45 градусов=4sqrt(3)*sqrt(2)/2=2sqrt(6)

V(пирамиды)=(1/3)*S(основания)*Н=
=(1/3)*S(квадрата АВСD)*SO=
=(1/3)*(2sqrt(6))^2*2=
=16