Задача 21048 ...

slava191

14.12.2017

а) Решите уравнение
cos^2(3x/2)+sin^2x = cos^2(3x/2)*sin^2x

б) Найдите сумму решений уравнения, принадлежащих отрезку [–5Pi; 5Pi].

SOVA

14.12.2017

★

0+0=0 ·0 – верное равенство,
значит
уравнение имеет решение если
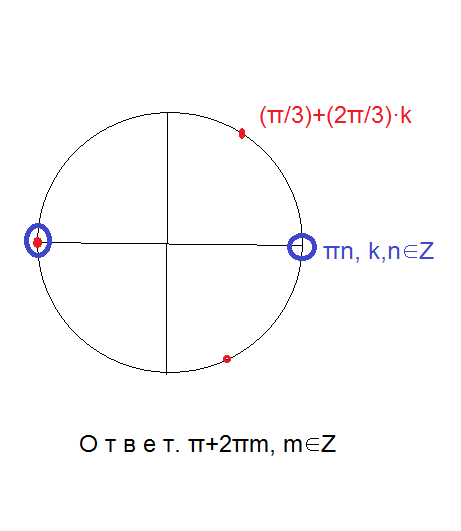
{cos(3x/2)=0 ⇒ 3x/2=(π/2)+πk, k∈Z x=(π/3)+(2π/3)·k, k∈Z
{sinx=0 ⇒ x=πn, n∈Z
Общие решения первого и второго уравнений
х=π+2πm, m∈Z
( см. рис.)

о т в е т
x=π+2πm, m∈Z

Делим на cos^2(3x/2) · sin^2x ≠ 0
(1/sin^2x)+(1/cos^2(3x/2))=1
Применяем формулы
1+сtg^2α =1/sin^2α
и
1+tg^2α =1/cos^2α
(1+ctg^2x)+(1+tg^2(3x/2))=1
ctg^2x+tg^2(3x/2)=–1
Уравнение не имеет корней.

О т в е т.
а)x=π+2πm, m∈Z
б) Указанному отрезку принадлежат корни
–5π; –3π; -π; π; 3π; 5π
Их сумма равна 0
В ответе 0