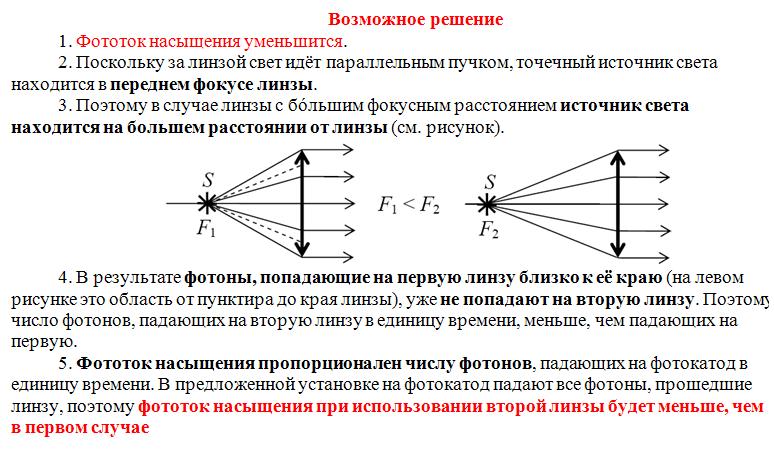
В установке по наблюдению фотоэффекта свет от точечного источника S, пройдя через собирающую линзу, падает на фотокатод параллельным пучком. В схему внесли изменение: на место первоначальной линзы поставили другую того же диаметра, но с бóльшим фокусным расстоянием. Источник света переместили вдоль главной оптической оси линзы так, что на фотокатод свет снова стал падать параллельным пучком. Как изменился при этом (уменьшился или увеличился) фототок насыщения? Объясните, почему изменяется фототок насыщения, и укажите, какие физические закономерности Вы использовали для объяснения.
физика 10-11 класс
4067