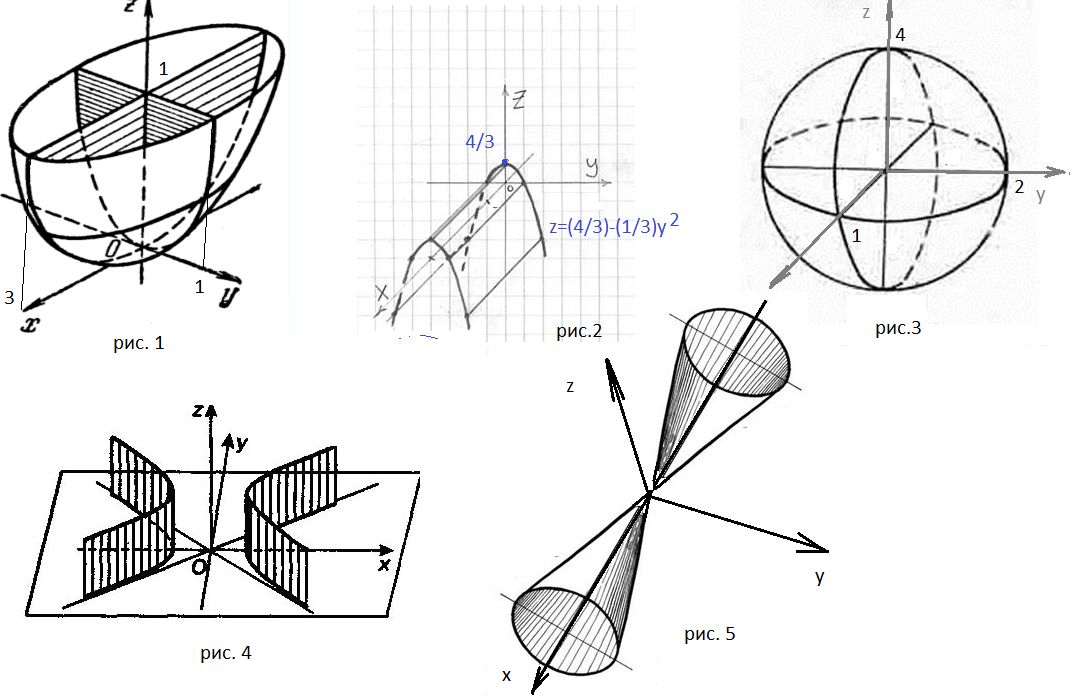
Задача 20954 5. Построить поверхности: 1)...
Условие
1) x^2+9y^2=9z
2) 3z=4-y^2
3) x^2+y^2/4+z^2/16 = 1
4) x^2-z^2=4
5) x^2=y^2+z^2
Решение
На плоскости хОу одна точка (0;0;0)
При z=1 в сечении эллипс (x^2/9)+y^2 =1
(''прижатый'' к оси ох)
2) z=(4/3) - (1/3)y^2 - параболический цилиндр.
Вершины парабол лежат на прямой, проходящей через точку (0;0;4/3) и параллельной пл. хОу.
Все параболы параллельны параболе z=(4/3) - (1/3)y^2, построенной в пл. yOz
3) Эллипсоид
a=1
b=2
c=4
4) (x^2/4)-(z^2/4)=1
- гиперболический цилиндр, образующие которого параллельны оси Оу.
Гипербола при на плоскости хОz
имеет вершины в точках (2;0;0) и (-2;0;0)
5) Конус вращения.
Сечения конуса, плоскостями, параллельные пл. уОz, окружности, радиусы которых с увеличением x по модулю, увеличиваются