Задача 209 Найдите наибольшее значение функции y =...
Условие
математика 10-11 класс
4097
Решение
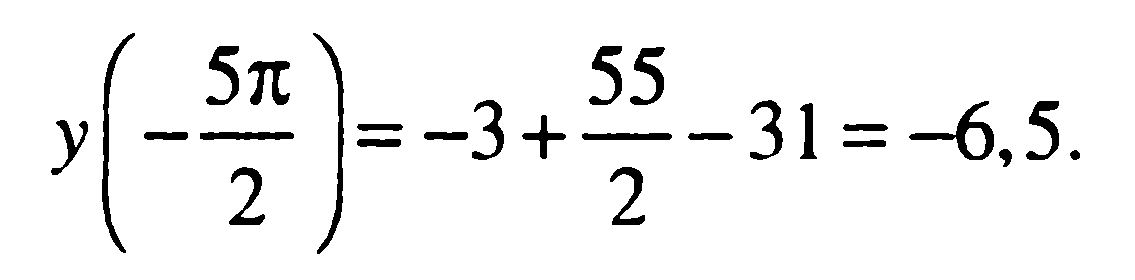
Ответ: -6,5
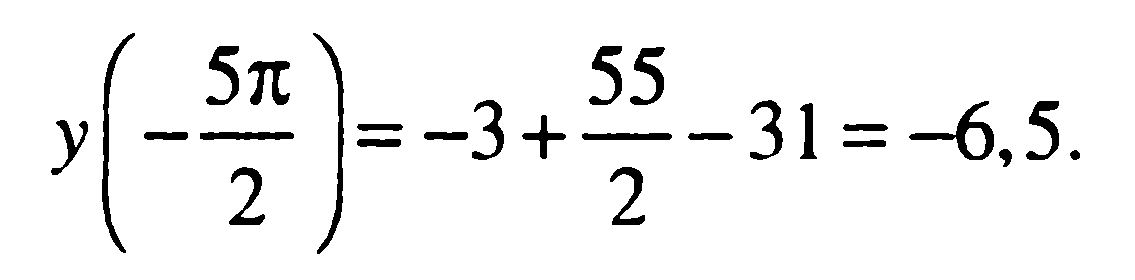
Ответ: -6,5