Задача 20880 ...

slava191

12.12.2017

Найдите больший угол четырёхугольника ABCD, вершины которого расположены на окружности, если известно, что ∠ABD=74 градуса, ∠DBC=38 градусов, ∠BDC=65 градусов. Ответ укажите в градусах.

SOVA

12.12.2017

★

Вписанный угол измеряется половиной дуги, на которую он опирается.
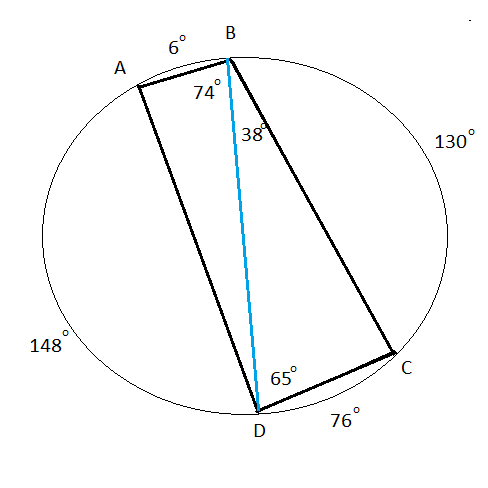
Значит, градусная мера дуги AD ( на нее опирается угол ABD)
74 градусов *2= 148 градусов.
градусная мера дуги DС ( на нее опирается угол DBC)
38 градусов *2= 76 градусов.
градусная мера дуги ВС ( на нее опирается угол BDC)
65 градусов *2= 130 градусов.

Окружность содержит 360 градусов.
Значит градусная мера дуги АВ=
360 градусов - 148 градусов - 130 градусов - 76 градусов=
6 градусов.
∠ ADC=3 градусов

Наибольший угол четырехугольника АВСD опирается на наибольшую дугу.
Дуга АВС 136 градусов
Дуга АDС 224 градусов - наибольшая дуга
Дуга DАВ 154 градусов
Дуга ВСD 206 градусов

На дугу ADC опирается угол B
О т в е т. ∠ В= 112 градусов