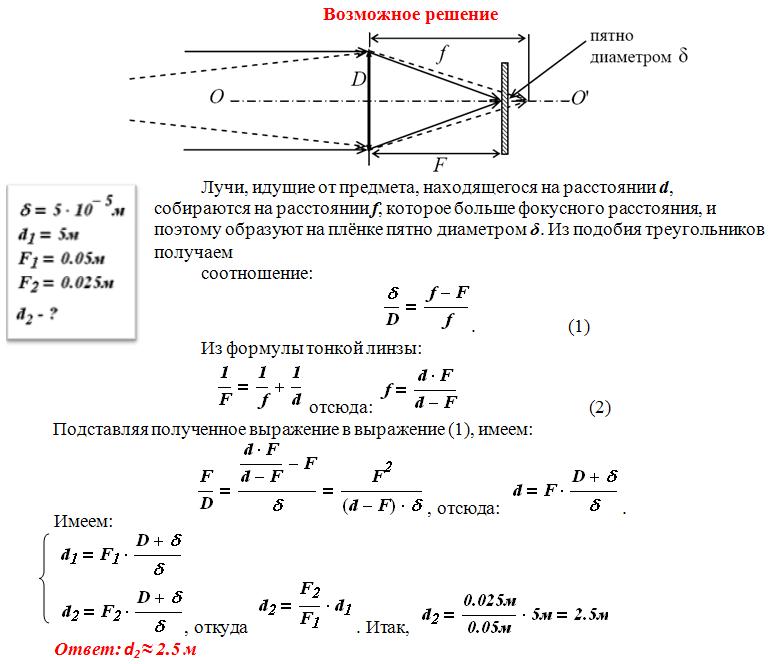
Объективы современных фотоаппаратов имеют переменное фокусное расстояние. При изменении фокусного расстояния «наводка на резкость» не сбивается. Условимся считать изображение на плёнке фотоаппарата резким, если вместо идеального изображения в виде точки на плёнке получается изображение пятна диаметром не более 0,05 мм. Поэтому если объектив находится на фокусном расстоянии от плёнки, то резкими считаются не только бесконечно удалённые предметы, но и все предметы, находящиеся дальше некоторого расстояния d. Оказалось, что это расстояние равно 5 м, если фокусное расстояние объектива 50 мм. Как изменится это расстояние, если, не меняя «относительного отверстия» изменить фокусное расстояние объектива до 25 мм? («Относительное отверстие» – это отношение фокусного расстояния к диаметру входного отверстия объектива.) При расчётах считать объектив тонкой линзой. Сделайте рисунок, поясняющий образование пятна.
физика 10-11 класс
6684