Задача 20491 ...

slava191

06.12.2017

Сфера касается рёбер BS, CS, CA, AB пирамиды SABC в точках K, L, M, N соответственно.

а) Докажите, что точки K, L, M, N лежат в одной плоскости.
б) Найдите KM, если KL = 8, LM = 8, MN = 6, NK = 4.

SOVA

06.12.2017

★

По свойству касательных, проведенных из одной точки:
AN=AM;BK=BN;CM=CL;SK=SL
Обозначим
AN=AM=a
BK=BN=b
CM=CL=c
SK=SL=d
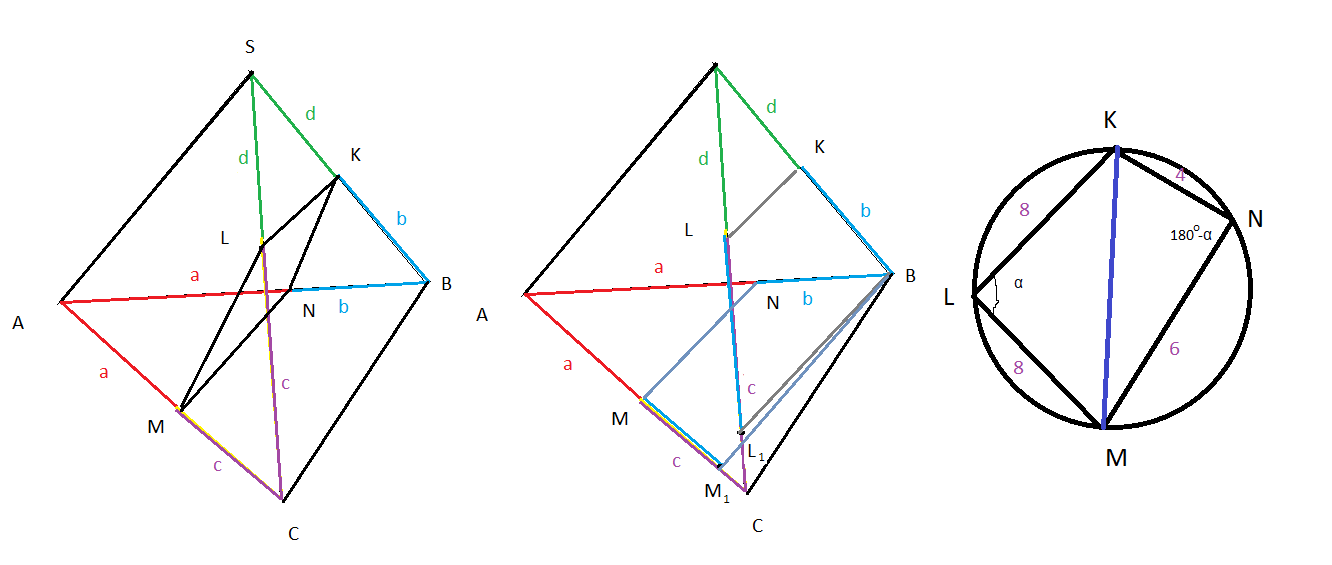
(cм. рис.1)
а)
Пусть b=c.
Тогда MN|| BC и KL|| BC, значит MN|| KL и четыре точки K, L,M,N лежат в одной точке.
пусть b < c
Тогда на СМ есть точка М_(1) такая, что ММ_(1)=b
и на СL есть точка L_(1) такая, что LL_(1)=b

AM_(1)=AB MN || M_(1)B
SL_(1)=SB LK || L_(1)B
( cм. рис.2)
Значит, прямые MN и LK пересекаются с ВС в точках P и Q
на продолжении ВС за точку В.

Рассматриваем подобные треугольники
ΔCBM_(1) подобен треугольнику СРМ
СМ_(1):СМ=СВ:СР
СР=(b/(c-b))CB
ΔCBL_(1) подобен треугольнику СQL
СL_(1):СL=СВ:СQ
СQ=(b/(c-b))CB

CQ=CP ⇒ точки Р и Q слвпадают.
Значит MN и KL пересекаются в точке P=Q и тем самым доказано, что четыре точки K, L, M, N лежат в одной плоскости.

Аналогично и в случае b > c.

б)
Четырехугольник KLMN вписан в окружность, значит сумма противоположных углов равна 180 градусов.
Обозначим
∠MLK=α
тогда
∠MNK=π-α
По теореме косинусов
KM^2=8^2+8^2-2*8*8cosα
KM^2=6^2+4^2-2*6*4cos(π-α)

KM^2=8^2+8^2-2*8*8cosα
KM^2=6^2+4^2+2*6*4cosα
Вычитаем из первого равенства второе
0=76-176cosα
cosα=19/44

KM^2=8^2+8^2-2*8*8*(19/44)
KM^2=8^2+8^2-2*8*8*(19/44)
KM=20sqrt(2/11)
О т в е т. б) 20sqrt(2/11)=20sqrt(22)/11