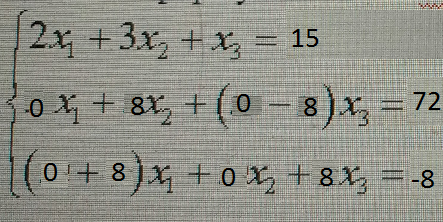Задача 20415 ...
Условие
N=8
Контрольная работа
Тема 1. Элементы линейной алгебры
1.1. Найти значение матричного многочлена (mE - nA) ⋅ B , если
[m] A = \begin{pmatrix} -2 & 0 \\ 3 & m \end{pmatrix}, \quad B = \begin{pmatrix} -1 & 0 & m+n \\ n & 5 & -3 \end{pmatrix}, \quad E = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}. [/m]
1.2. Решить систему линейных алгебраических уравнений двумя способами: по формулам Крамера и методом Гаусса:
[m] \begin{cases}
2x_1 + 3x_2 + x_3 = 2m + 2n - 1 \\
mx_1 + nx_2 + (m - n)x_3 = m^2 + n^2 - m + n \\
(m + n)x_1 + mx_2 + nx_3 = m^2 + 2mn - n
\end{cases} [/m]
Решение
{8x_(2)-8x_(3)=72
{8x_(1)+8x_(3)=-8
{x_(1)=-1-x_(3)
{x_(2)=9+x_(3)
подставляем в первое
2*(-1-х_(3))+3*(9+х_(3))+х_(3)=15
2х_(3)=-10
х_(3)=-5
х_(1)=4
х_(2)=4