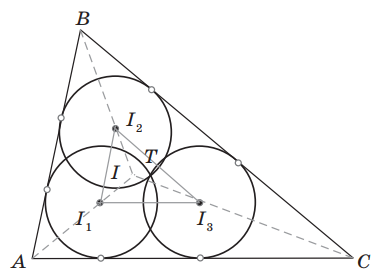
Дан треугольник ABC, в котором расположены три равные окружности ω_(1), ω_(2), ω_(3), с центрами в точках I_(1), I_(2), I_(3), проходящие через общую точку T. Окружность ω_(1) касается сторон AB и AC, окружность ω_(2) касается сторон BA и BC, окружность ω_(3) касается сторон CB и CA. Обозначим I — центр окружности, вписанной в треугольник ABC, а O — центр окружности, описанной около треугольника ABC.
а) Докажите, что точки I, T, O лежат на одной прямой.
б) Найдите радиус трёх равных окружностей, если стороны треугольника ABC соответственно равны 13, 14, 15.
математика 10-11 класс
2712