Задача 19743 Решить неравенство (x^2+x+1)^(x^2-5x+6)...
Условие
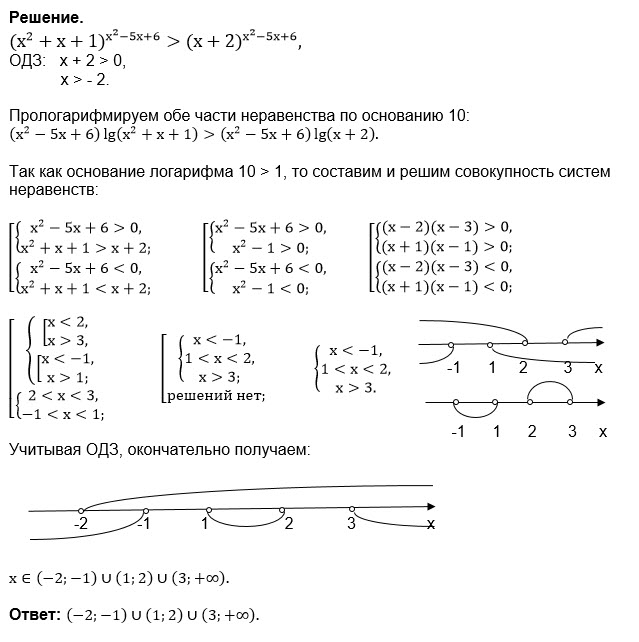
Решение
{x^2+x+1 > 0 ⇒ x ∈(- бесконечность; + бесконечность), D < 0
{x+2 > 0 ⇒ x > -2
ОДЗ: х∈(- 2; + бесконечность)
Делим обе части уравнения на (х+2)^(x^-5x+6).
((x^2+x+1)/(x+2))^(x^2-5x+6) > 1
Рассматриваем два случая
1) (x^2+x+1)/(x+2) > 1
Показательная функция с основанием больше 1 возрастающая. Большему значению функции соответствует большее значение аргумента
x^2-5x+6 > 0
Система неравенств:
{(x^2+x+1)/(x+2) > 1⇒(x^2+x+1-x-2)/(x+2) > 0⇒ (-2;-1)U(1;+бесконечность)
{x^2-5x+6 > 0 ⇒ (-бесконечность;2)U(3;+бесконечность)
Ответ 1) (-2;-1)U(1;2)U(3;+бесконечность)
удовлетворяет ОДЗ
2) 0 < (x^2+x+1)/(x+2) < 1
Показательная функция с основанием меньше 1 убывающая. Большему значению функции соответствует меньшее значение аргумента
x^2-5x+6 < 0
Система неравенств:
{(x^2+x+1)/(x+2) < 1⇒(x^2+x+1-x-2)/(x+2) < 0⇒(-бесконечность;-2)U(-1;1)
{x^2-5x+6 < 0 ⇒ (2;3)
Ответ 2) нет решений
О т в е т. (-2;-1)U(1;2)U(3;+бесконечность)
Все решения