Задача 19742 а) Решите уравнение...

slava191

20.11.2017

а) Решите уравнение log(ctgx)(3+2cos2x+2cos4x) = 0,

б) Найти корни уравнение на отрезке [0; Pi]

SOVA

25.11.2017

★

ОДЗ:
{3+2cos2x+2cos4x > 0
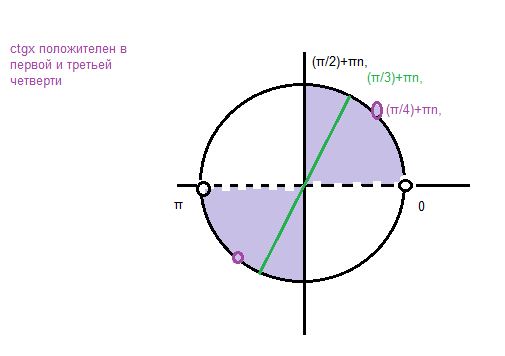
{ctgx > 0, ctgx ≠1

По определению логарифма
3+2сos2x+2cos4x=(ctgx)^0 ( согласовано с первым неравенством ОДЗ, (ctgx)^0=1 > 0)
Так как
cos4x=2cos^22x-1, уравнение принимает вид
3+2сos2x+2*(2cos^22x-1)=1
4cos^22x+2cos2x=0
2cos2x*(2cos2x+1)=0
cos2x=0 или 2сos2x+1=0
2x=(π/2)+πk, k∈Z или 2х=±(2π/3)+2πn, n∈Z
x=(π/4)+(π/2)k, k∈Z или х=±(π/3)+πn, n∈Z

Согласно ОДЗ ctgx больше или равно 0, сtgx ≠1, поэтому x=(π/4)+(π/2)k, k∈Z не удовл ОДЗ
х=-(π/3)+πn, n∈Z не удовл ОДЗ.
О т в е т. а) х=(π/3)+πn, n∈Z
б)(π/3) - корень, принадлежащий отрезку [0;π],