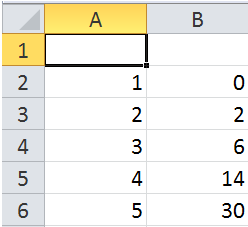
В электронной таблице ячейки диапазона A2:A6 последовательно заполнены натуральными числами от 1 до 5. В ячейку B2 записали формулу =ОСТАТ($A$1;СТЕПЕНЬ(2;A2)). Затем содержимое ячейки B2 последовательно скопировали в ячейки диапазона B3:B6. Получились следующие значения:
Сколько существует натуральных чисел меньших 256, которые могут быть занесены в ячейку A1, чтобы результат вычисления формул давал результат, указанный на рисунке и чему будет равно минимальное из этих чисел? В ответе укажите через один пробел два целых числа: сначала минимальное из них, а затем количество найденных чисел.
предмет не задан
6409
Данную задачу можно решать как аналитически, так и средствами электронных таблиц. При решении средствами электронных таблиц можно осуществить подстановку всего диапазона натуральных чисел меньших 256, то есть 1-256 в заданную в условии формулу =ОСТАТ($A$1;СТЕПЕНЬ(2;A2)) и посчитать количество совпадений с ответом приведенным в столбце В. Для этого можно в ячейках С1-IX1 задать искомый диапазон 1-256, воспользовавшись инструментом заполнения значений ячеек в виде арифметической прогрессии. Затем в ячейке С2 задать формулу =ОСТАТ(C$1;СТЕПЕНЬ(2;$A2)), распространить ее на диапазон С3:С6. В ячейке С7 задать формулу =ЕСЛИ(И($B$2=C2;$B$3=C3;$B$4=C4;$B$5=C5;$B$6=C6);1;0), которая позволит вычислить полное совпадение полученого столбца с образцом заданным в столбце В. Затем распространить ячейки диапазона С2:С7 на диапазон D:IX. Посчитав сумму диапазона значений ячеек С7:IX7 получим искомое количество натуральных чисел удовлетворяющее условию заданных остатков, а максимальное из них можно определить визуально по значению первой строки в последнем столбце, содержащем 1 в седьмой строке. Таким образом получаем ответ: 8 254. Примечение. Если используемые электронные таблицы не позволяют заполнять более 256 столбцов, задачу можно решить в два этапа, отдельно проверив последние несколько значений. Аналитическое решение: Проведем анализ заданной формулы: =ОСТАТ($A$1;СТЕПЕНЬ(2;A2)); Можно говорить о том, что диапазон А2:А6 задает делители 2,4,8,16, 32 соответственно. Таким образом, можно говорить, что искомые числа, удовлетворяющие заданным в ячейках диапазона В2:В6, будут четными (остаток от деления на 2 равен 0) и минимальное из них будет равно 30 (0+30=30), поскольку это первое число удовлетворяющее остатку заданному в ячейке В6, проверим для полученного числа остальные значения — они полностью удовлетворяют условию (В2:В5). Следовательно, нам необходимо искать все числа большие 30, но меньшие 256, с шагом 32, получаем ряд: 30, 62, 94, 126, 158, 190, 222, 254. 14
