Задача 19338 Дано уравнение cosx+1/cosx+cos^2x+tg^2x...

slava191

11.11.2017

Дано уравнение cosx+1/cosx+cos^2x+tg^2x = 3/4

A) Решите уравнение.
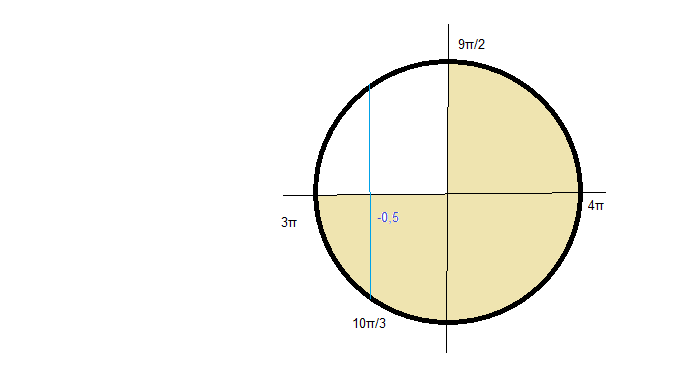
Б) Укажите корни этого уравнения, принадлежащие отрезку [3Pi; 9Pi/2]

SOVA

11.11.2017

★

cosx ≠ 0 ⇒ x ≠ (Pi/2)+Pik, k ∈ Z

tg^2x=sin^2x/cos^2x
(cos^3x+cosx+cos^4x+sin^2x)/cos^2x=3/4
4cos^4x+4cos^3x-7cos^2x+4cosx+4=0
Разложим на множители левую часть уравнения
(cosx+2)*(cosx+0,5)*(4cos^2x-6cosx+4)=0
cosx=-2 - уравнение не имеет корней
квадратное уравнение относительно косинуса
4cos^2x-6cosx+4=0 имеет отрицательный дискриминант,
cosx=-0,5
x=± (2π/3)+2πn, n∈Z
О т в е т.
А) ± (2π/3)+2πn, n∈Z
Б) Указанному промежутку принадлежит корень
х=- (2π/3)+4π=10π/3