Задача 19332 Периметр правильного треугольника равен...
Условие
математика 10-11 класс
18633
Решение
★
AB+BC+AC=24sqrt(3)
АВ=ВС=АС=24sqrt(3)/3=8sqrt(3)
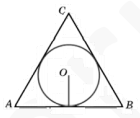
AO-биссектриса, ∠ ОАК=30 градусов.
ОК ⊥ АВ
Из прямоугольного треугольника АОК
r=ОК=AK*tg 30 градусов=(1/2)АВ*tg 30 градусов=
4sqrt(3)*(1/sqrt(3))=4 Δ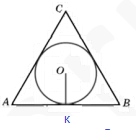
Все решения
тогда из условия следует а=Р/3, а=24sgrt(3)/3=8sgrt(3).
В равностороннем треугольнике радиус вписанной окружности равен r=a*sgrt(3)/6. отсюда
r=8sgrt(3)*sgrt(3)/6=8*3/6=4.
Ответ:4.
