Задача 18794 Найти предел функции ...
Условие
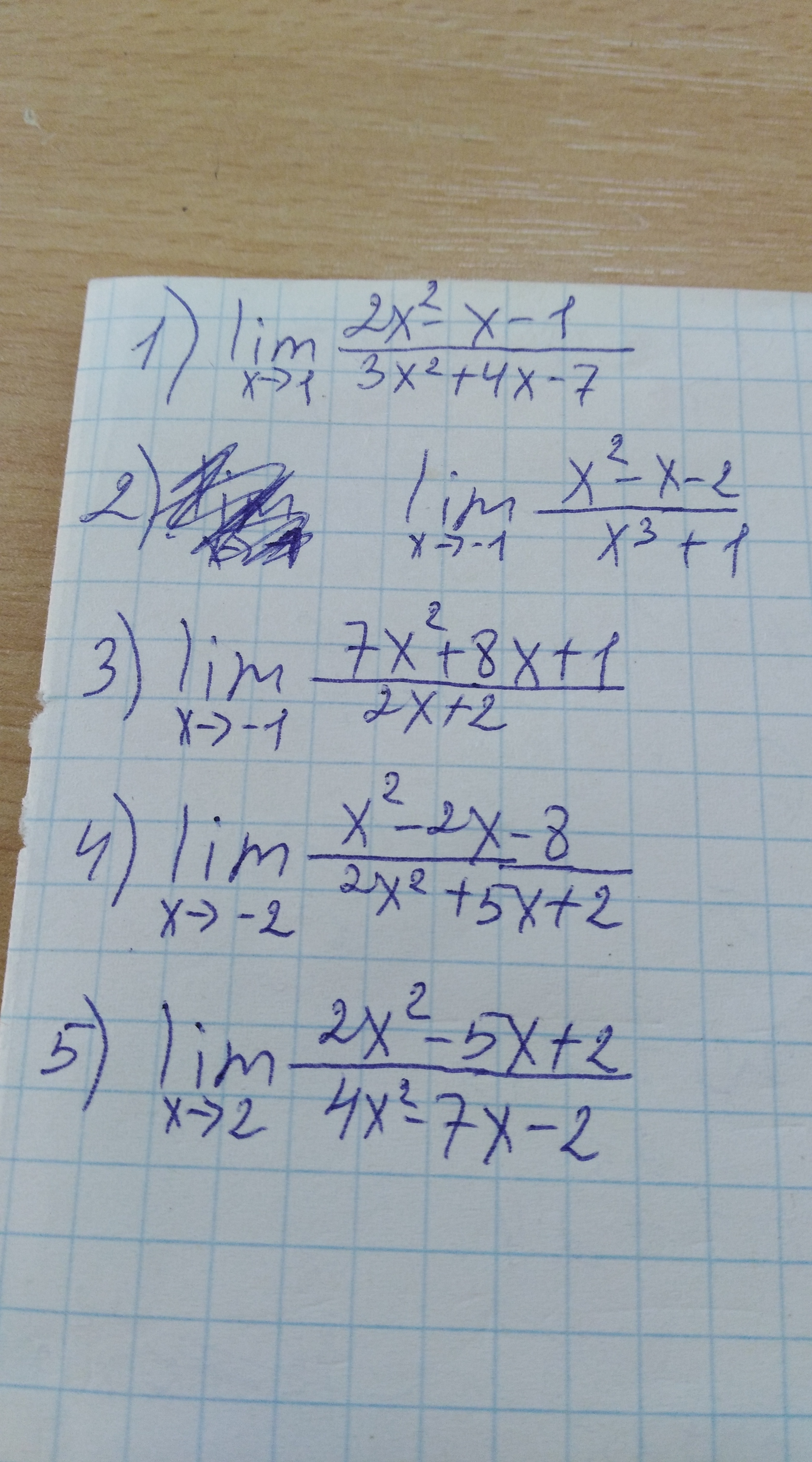
Решение
(2-1-1)/(3+4-7)=0/0
неопределенность
Устраняем.
Раскладываем и числитель и знаменатель на множители
(2х+1)(х-1)/(3х+7)(х-1)= х только стремится к 1 , но х ≠ 1, поэтому х-1 ≠ 0 и на множитель (х-1) можно сократить и числитель и знаменатель.
Остается найти предел дроби
(2х+1)/(3х+7)
Подставляем х=1 получаем (2*1+1)/(3*1+7)=3/10
О т в е т. 3/10
2)
0/0
(х+1)(х-2)/(х+1)(х^2-х+1)
Сокращаем на (х+1)
Находим предел дроби
(х-2)/(x^2-x+1) непосредственно подставляя х=-1
О т в е т. (-1-2)/(1+1+1)=-1
3)0/0
(х+1)(7х+1)/2(х+1)
Сокращаем на (х+1)
Находим предел дроби
(7х+1)/2 непосредственно подставляя х=-1
О т в е т. (-7+1)/2=-3
4)0/0
(х+2)(х-4)/(х+2)(2х+1)
Сокращаем на (х+2)
Находим предел дроби
(х-4)/(2x+1) непосредственно подставляя х=-2
О т в е т. (-2-4)/(-4+1)=2
5)0/0
(2х+1)(х-2)/(х-2)(4х+1)
Сокращаем на (х-2)
Находим предел дроби
(2х+1)/(4x+1) непосредственно подставляя х=2
О т в е т. (4+1)/(8+1)=5/9