Основанием треугольной пирамиды SABC является прямоугольный треугольник AВС с гипотенузой АВ = 13 и катетом АС = 5. Высота пирамиды равна 3. Найдите объем пирамиды.
математика 10-11 класс
7816
Прежде всего, обратим внимание на вопрос, который поставлен в условии задачи. Объем пирамиды равен одной трети произведения площади основания пирамиды на ее высоту. Поэтому основные события разворачиваются в основании пирамиды, площадь которого надо найти. Площадь прямоугольного треугольника равна половине произведения катетов. Один из катетов равен 5, а по теореме Пифагора найдем, что длина второго катета равна 12. Итак, площадь основания равна 30, а объем пирамиды равен 30.
[b]Нормальное решение[/b]
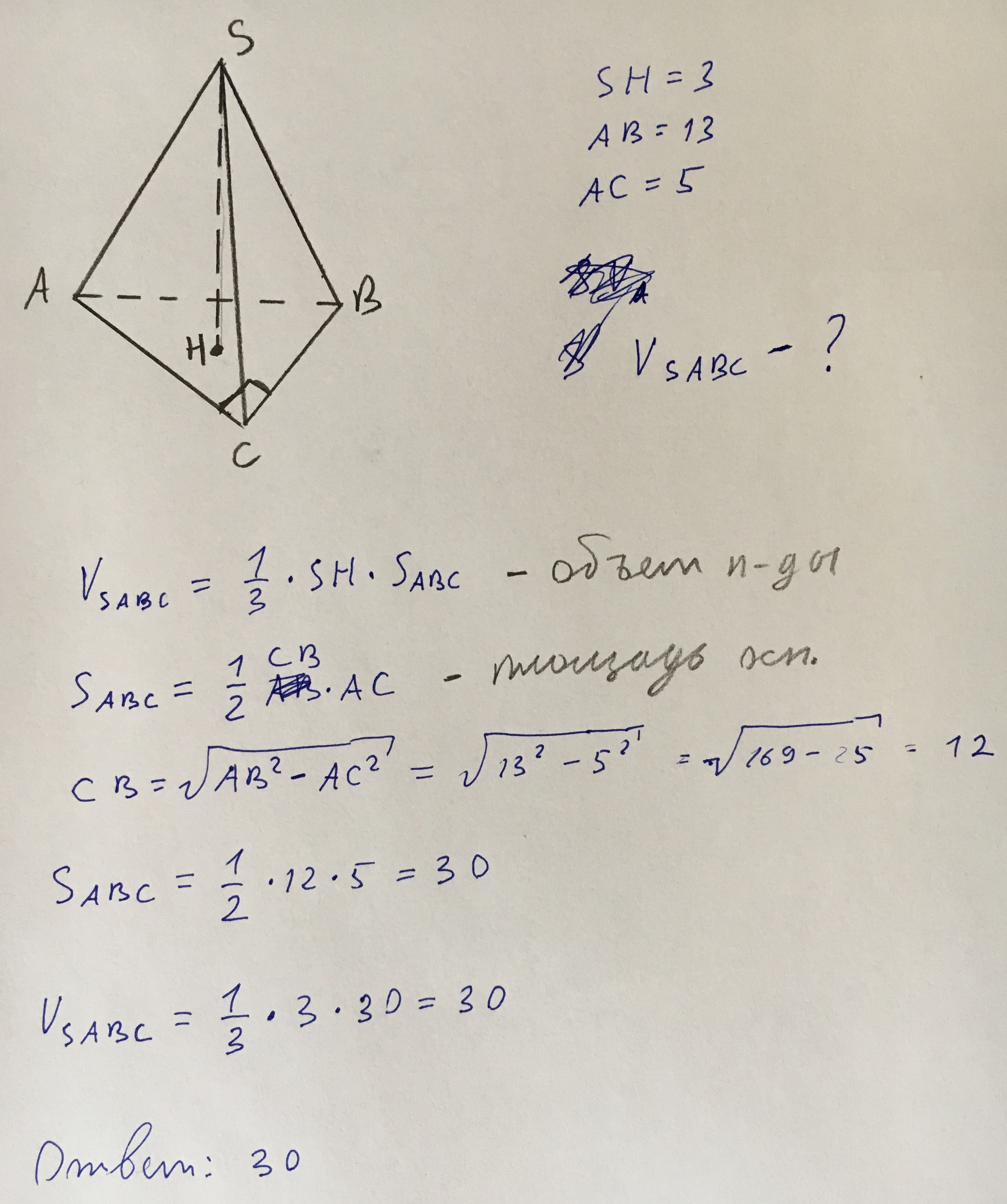
Ответ: 30

