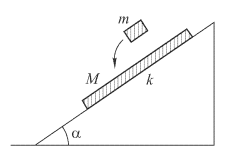
По наклонной плоскости, составляющей угол а с горизонтом, ускоренно скользит доска массы М. Коэффициент трения доски о наклонную плоскость равен k. На доску кладут тело массы m, которое скользит по доске без трения. Какова должна быть минимальная масса тела mмин, чтобы движение доски по наклонной плоскости стало равномерным?
физика 10-11 класс
11758
Уравнение движения доски при условии, что тело скользит по ней без трения, имеет вид
Ma = Mgsin a — (М + m)kg*cosa.
Полагая а = 0, находим mмин = M*((tga-k)/k). При m > mмин доска остановится.
Ответ: mмин = M*((tga-k)/k)
Вопросы к решению (2)
как вы определили N - СИЛУ НОРМАЛЬНОГО ДАВЛЕНИЯ
N - это сила реакции опоры. Обычно определяют как mg умноженная на синус или косинус альфа, где альфа - угол между вектор этой силы и иксовой осью по которой происходит движение
Предыдущее решение, простите?
