Задача 18514 Найти:...
Условие
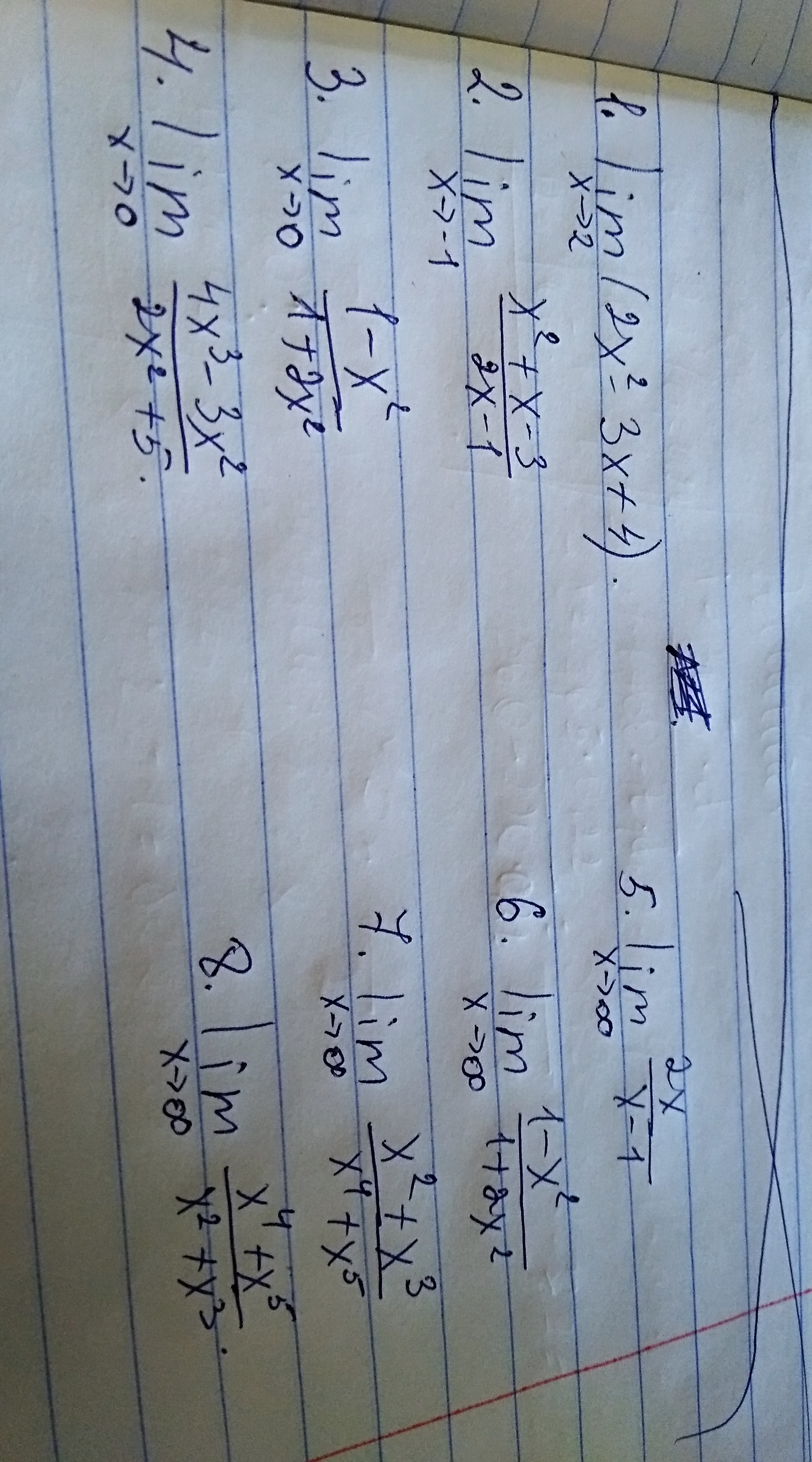
Решение
2*(2^2)-3*2+4=3
О т в е т. 3
2)подставляем значение х=-1 в выражение под знаком предела.
((-1)^2+(-1)-3)/(2*(-1)-1)=(-5)/(-3)=5/3
О т в е т. 5/3
3)подставляем значение х=0 в выражение под знаком предела.
(1-0^2)/(1+2*0^2)=1/1=1
О т в е т. 1
4)подставляем значение х=0 в выражение под знаком предела.
(4*0^3-3*0^2)/(2*0^2+5)=0/5=0
О т в е т. 0
5) подставляем х=бесконечность в выражение под знаком предела.
Получаем (бесконечность/бесконечность) - неопредленность
Устраняем неопределенность.
Делим и числитель и знаменатель на х
Получаем 2/(1-(1/x))
Если х→∞, то х - бесконечно большая величина, тогда обратная ей (1/х)- бесконечно малая.
(1/х)→∞
Получаем ответ
2/(1-0)=2
О т в е т. 2
6) как 5)
Делим на х^2
((1/x^2)-1)/(1+2*(1/x^2))=(0-1)/(0+2)=-1/2
7) Делим на x^5 ( в самой высокой степени из имеющихся в данном выражении)
((1/x^3)+(1/x^2))/((1/x)+1)=(0+0)/(0+1)=0
8) Дробь в 8) обратная той, которая написана в 7)
Значит если в 7) получилось в ответе бесконечность , бесконечно много, то в этом ответе 0 ( бесконечно мало)